Критерий оптимальности

Рис.4

Рис.1

Измененное устройство выдает информацию (в том числе и управляющему устройству) о текущем состоянии объекта. Если на основании вектора измерений 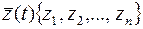могут быть найдены значения всех координат состояния 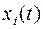, не могут быть найдены при известном значении вектора измерений 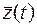, то система будет не полностью наблюдаемой. Управляющее устройства вырабатывает управляющее воздействие 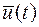. Таких управляющих воздействий будет несколько, поэтому полагаем, что вектором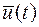 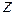- мерный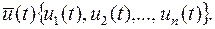

На вход управляющего устройства поступает задающее воздействие 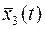, которое содержит инструкцию о том, каково должно быть состояние объекта 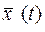- так называемое «желаемое состояние».

На объект управления может поступать возмущающие воздействие 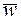, представляющие нагрузку или помеху. Измерение координат объекта измерительным устройством может производиться с некоторыми случайными погрешностями 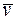, называемыми шумами измерения.

Задачей управляющего устройства является выработка такого управляющего воздействия 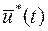, чтобы качество функционирования САУ в целом было бы наилучшим в некотором смысле.

В дальнейшем будем рассматривать только те объекты, которые являются управляемыми, т.е. вектор состояния которых можно изменять требуемым образом путем соответствующего измерения вектора управления. Кроме того, объект предполагается полностью наблюдаемым, т.е. в этом случае, очевидно, можно не делать разницы между векторам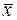и и .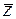

Отметим, что в дальнейшем измеряемые внешние воздействия 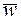и 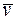при рассмотрении задач управления для упрощения задачи не учитывается. Кроме того мы ограничимся рассмотрением объектов, динамика которых описывается обыкновенными дифференциальными уравнениями. С учетом всего сказанного функциональная схема САУ может быть приведены к виду рис.2

рис.2

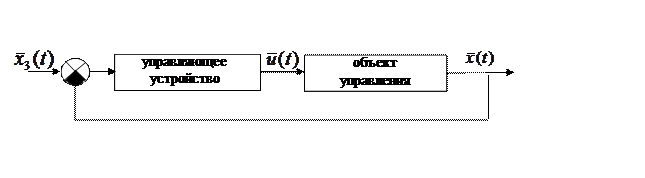
Уточним и конкретизируем постановку задачи оптимального управления. Ранее при обсуждении типовых задач ОУ 5 и 6, речь шла об несколько абстрактных понятиях – управления связи.

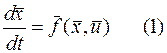, где

и задавалось начальное 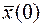и конечное 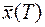значения вектора .

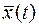Сейчас учетом сказанного можем считать, что уравнения связи это не что иное как дифференциальные уравнения объекта управления, методика получения которых рассматривается в курсе ТАУ.

Существует много различных путей решения рассматриваемой задачи. Но только один способ управления объектом дает наилучший в некотором смысле результат. Этот способ управления и реализующую его систему называют оптимальными.

Чтобы иметь количественные основания для предпочтения одного способа управления всем другим, необходимо определить цель управления, а затем ввести меру, характеризующую эффективность достижения цели –критерий оптимальности управления. Обычно критерий оптимальности- это числовая величина, зависящая от изменяющихся во времени и пространстве координат и параметров системы так, что каждому закону управления соответствует определенное значение критерия. В качестве критерия оптимальности могут быть выбраны различные технические и экономические показатели рассматриваемого процесса.

Иногда к системе управления предъявляются различные, подчас противоречивые требования. Законы управления, который одновременно наилучшим образом удовлетворял бы каждому требованию, не существует.

Поэтому из всех требований нужно выбрать одно главное, которое должно удовлетворяться наилучшим образом. Другие требования играют роль ограничений.

Следовательно, выбор критерия оптимальности должен производиться, только на основании изучения технологии и экономики рассматриваемого объекта и среды. Эта задача выходит за рамки теории ОУ.

В качестве критерия, характеризующего качество процесса управления, чаще всего выбирается функционал

или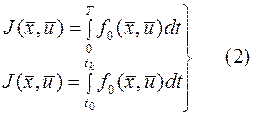

Относительно подынтегральной функции 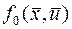будем предполагать, что она непрерывна по всем аргументам и имеет непрерывные частные производные по переменным .

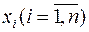Для выполнения задачи управления мы располагаем ограниченными энергетическими и материальными ресурсами. Учет ограничений, естественно, стесняет выбор закона управления и одновременно делает задачу более определенной. Некоторые задачи более определенной. Некоторые задачи, сформулированные без учета ограничений, вообще не имеют смысла.

Например, задача о предельном воздействии в линейной системе (в случае с нажимным устройством прокатного стана) при неограниченных управляющих воздействиях лишена смысла. Время процесса в этом случае будет равно нулю, а воздействия бесконечны.

Математически ограничения часто имеют вид неравенств, относящихся к координатам, управляющим воздействиям или их функциям. Например, используемая нами ранее в типовой задаче «6» запись

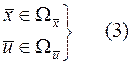
Носит достаточно абстрактный характер, говорит лишь о том, что соответствующая величина не может или не должна выходить за допустимые границы, вид которой здесь конкретизирован. Чаше всего эта граница задается многомерным параллелепипедом

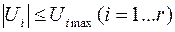
Так, например, для 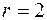параллелепипед предстает прямоугольником, за границы которого конец вектора управления не должен выходить. Такое управление называется допустимым.

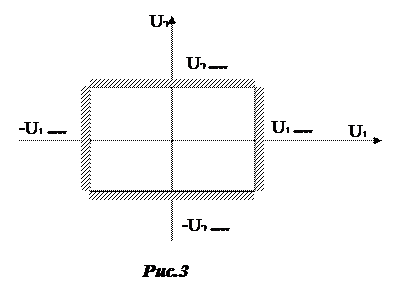
Максимально допустимые значения координат или воздействий определяются характеристиками технологического процесса и оборудования. Заметим, что учет ограничений – существенно влияет на постановку задачи об оптимальном управлении.

Основную задачу определения оптимального управления можно сформировать следующим образом.

В фазовом пространстве 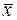заданы 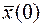начальное и 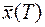конечное состояния ОУ. Среди всех допустимых управлений 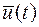, для которых соответствующих траектории проходят через начальное и конечное состояния (если такие управления существуют), необходимо выбрать такое 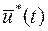, для которого функционал (2) принимал минимальное (максимальное) значение.

Проиллюстрируем сказанное. Рассмотрим два пространства- управлений и состояний для .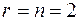

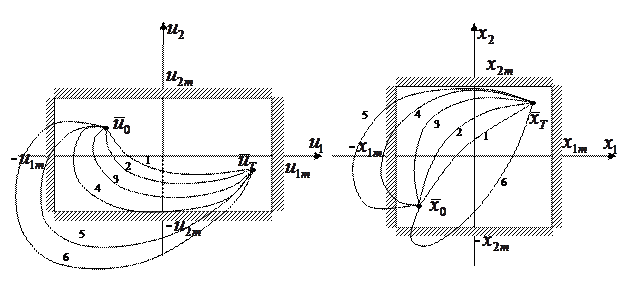
Отметим в них начальное и конечное состояние векторов состояние управления

Кривые 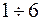в пространстве управлений есть фазовые траектории вектора управления фазовые траектории вектора управления. Траектории 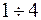допустимые траектории 5,6 –недопустимые т.к. выходят за область ограничений. Аналогично в пространстве состоящие фазовые траектории состояний 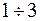допустимые, а 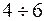недопустимые. Предполагается, что фазовой траектории под определенным номером в пространстве управлений соответствует фазовая траектория в пространстве состояний под тем же номером. Требуется из допустимых управлений 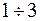(кривая 4 не рассматривается, т.тк.ая 4 нерассматривается авлений ом. тствует фазовая траекттория к. она вызывает недопустимую траекторию состояния 4) выбрать такую, которая, вызывает допустимые траектории состояния доставляет экстремум функционалу (2).

Это шестая типовая задача у управления, как уже отмечалось выше, называется неклассической вариационной задачей оптимального управления. Если же ограничения на координаты и управления (3) отсутствуют, и все вектора управления и состояния являются допустимыми, то возникает пята я типовая задача или классическая вариационная задача оптимального управления, (исследованию которой и посвящена настоящая глава).

Второй важной задачей оптимального управления является синтез оптимального регулятора, т.е. определение оптимального управления 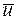как функции либо вектора наблюдения 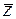, либо вектора состояния объекта 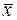, а не 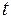, как мы только что рассматривали.

Выше уже говорилось, что в теории оптимального управления в качестве критериев оптимальности, как правило, применяются интегральные функционалы вида (2). В зависимости от вида подынтегральной функции 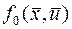могут быть получены различные критерии оптимизации, применяемые в практике проектирования оптимальных САУ.

Одним из наиболее распространенных критериев, для которого методика синтеза оптимального управления достаточно хорошо разработана, является время переходного процесса объекта управления из начального состояния 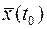в конечное 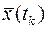. Этот критерий представляет собой частный случай функционала (2) при 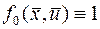тогда

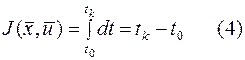
Казалось бы логично пользоваться интегральным критерием вида

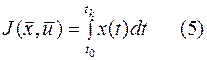, где

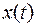- отклонения регулируемой координаты от нового установившегося значения, которое она будут иметь после завершения переходного процесса.

Геометрически интеграл (5) интегрируется как площадь под кривой 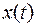. Эта площадь, а, следовательно, и величина критерия оптимальности, будет тем меньше, чем быстрее затухает переходной процесс и чем меньше величина отклонения в совокупности. Значит управление системой 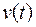надо выбирать так, что минимизировать критерий (5). Неудобством этой интегральной оценки является то, что она годится только для монотонных процессов, когда не меняется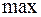 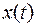. Если же имеет место колебательный процесс рис.5, то при вычислении интеграла (5) площади будут складываться алгебраически и минимум этого интеграла может соответствовать колебаниям с малым затуханием или вообще без затухания. Что избежать риски подобных ситуаций, следует использовать квадратичный, интегральный функционал

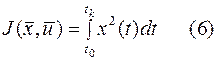
который не зависит от знаков отклонений, а значит и от формы переходного процесса (монотонный или колебательный).

Если при проектировании системы оптимального управления ставится задача ограничить резкие изменения выходной переменной во время изменения переходного процесса, при которых 1-ая производная может принимать достаточно большие значения, используется функция:

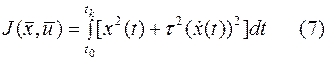, где

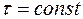- весовой коэффициент.

Минимизация этой формулы означает, что составляющая 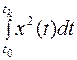запрещает значительные отклонения 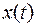от установившегося значения, составляющая 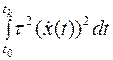запрещает существование больших производных 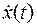. Таким образом, получается не только быстрый, но и плавный, без разных колебаний переходной процесс. Иногда для этих целей применяется и более сложные оценки вида:

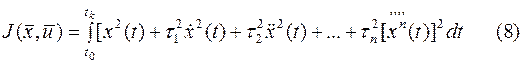
Вообще же квадратичные критерии широко распространенные в теории оптимального управления в самом общем случае содержат и члены зависящие от вектора управления, и слагаемое, учитывающие конечное состояние системы

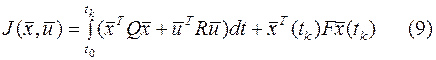
где 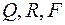- симметрические матрицы размера, соответственно 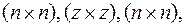а индекс «Т» означает операцию транспонирования.

Отметим, что элементов матрица 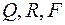определяет также технические показатели качества САУ, как перерегулирования время 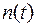, точность и т.д. В настоящее время разработана методика синтеза линейных САУ по квадратичному критерию (9), которая дает возможность получить структуру и параметры оптимального регулятора, т.е. решить задачу синтеза.

Функция другого вида

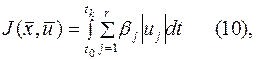где

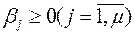- некоторые весовые коэффициенты, позволяют учесть расход рабочего тела на уравнение. Задачи, в процессе решения которых минимизируется функционал (10), называются задачами оптимизации САУ по расходу топлива. Такие задачи возникают, например, при управлении космическими аппаратами, когда существенным является экономичное расходование ограниченного количества горючего, имеющегося на борту.

В некоторых случаях рассматривают задачу минимизации функционала вида

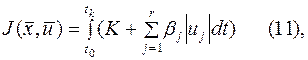где

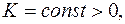
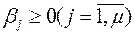, который представляет собой комбинацию функционалов (4) и (10)- позволяет учесть как время 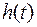, так и расход топлива.

Выбор того или иного функционала определяется техническими показателями и условиями работы проектируемой САУ и во многом зависит от инструкции и опыта инженера – проектировщика.