Метод Вольфа

Рис.1

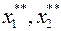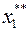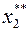Теперь – принадлежит ли точка многоугольнику ограничений. Подставим и в .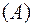

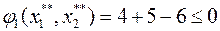т.к. 3>0 условие не выполняется.

И так, точка абсолютного 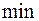не принадлежит многоугольнику, то решение задачи на условном 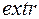может быть только на границе многоугольника ограничений, в данном примере.

На каком ребре 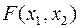достигает своего 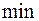? Если многоугольник имеет не слишком большое число ребер, вершин и граней, то решение можно найти простым перебором их. Можно сделать это методом Лагранжа.

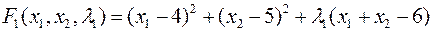
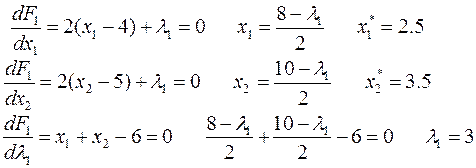
Проверим, выполняются ли для 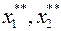другие ограничения.

- выполняются

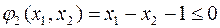
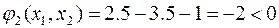выполняются.

Значит, точка 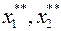может быть решением данной задачи. Вычисляем в этой точке значения .

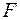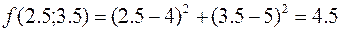
Теперь проверим с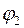

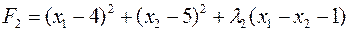
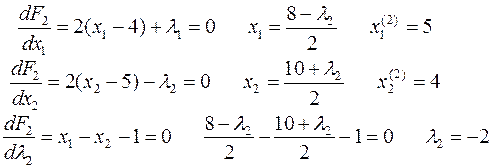
Проверим выполнение ограничения

выполняется.

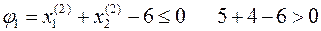не выполняются, следовательно, точки 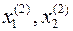не являются решением.

Затем проверяем пересечение с ребрами многоугольника.

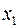и 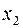- являются осями.

С осью 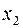точка 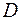имеет координаты

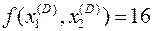, т.е. больше чем .

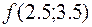Т.е. вообще не принадлежит многоугольнику. Далее проверяем нет ли решения в вершинах многоугольника?

Вершины (0) (1) (2) (3)

Значение 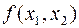41 17 6,5 9+25=34

Сравним значения 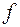со значениями 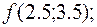находим, что

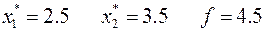является решением задачи.

Как это способ решения распространить на выпуклом программировании? Т.е. область ограничений выпукла. Её можно аппроксимировать многогранником и решать, как предыдущую квадратичную задачу. Решение получится приближенным. Следует иметь в виду, что задача аппроксимации в многомерном пространстве является весьма сложной задачей.

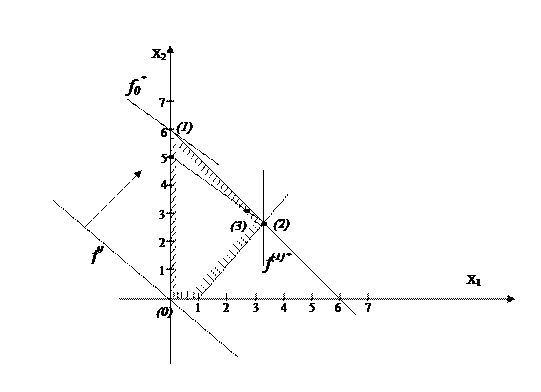
Идея метода Вольфа.

Раньше мы перебирали ребра, вершин и т.д. нельзя ли этот набор сделать целенаправленным, так чтобы за малое число итераций локализовать место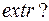

Метод начинается с выбора любой точки на многоугольнике ограничений. Возьмем в качестве начальной точки вершину 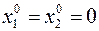. Линеаризуем 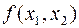, т.е. разложим в ряд Тейлора и ограничимся линейными членами.

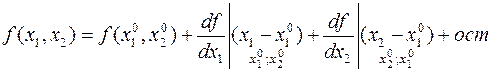
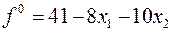
1. Найдем 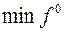на данном многоугольнике, а это Задача линейного применения. Перемещение 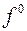параллельной самой себе при росте 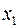и 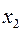, что видно из 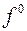ведет к 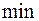. Получим 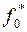, проходящую через точку (0;6).

Далее соединяем точку (0;6) с начальной точкой (откуда мы начинали). В данном примере эта линия совпадает с 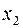т.к. многоугольник выпуклый, то эта линия принадлежит выпуклому множеству.

2. Ищем 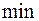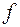(уже не линеаризованной) на этой линии т.е. задача Лагранжа: 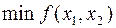на ребре (0;6).

Не приводя вычислений, получим этот 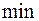в точке (0,5).

3. Линеаризуем 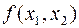в точке (0,5) получим 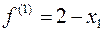. Найдем 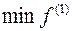на многоугольнике, получим 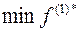в вершине (2).

4. Соединяем вершину (2) с точкой (0;5) получим ребро (0;5)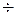(2). Ищем 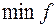на этом ребре. Получим точку (3).

5. Линеаризуем 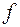в точке (3). Решаем задачу линейного программирования на многоугольнике. Получим 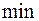в точке (1). Соединяем (1) и (3) и т.д., приближаясь к 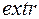точке на ребре (1)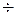(2)многоугольника.

Существуют и другие модификации метода симплексных процедур.