2015-01-21
494
Туннельным эффектом называется прохождение частицы сквозь потенциальный барьер – ограниченную область пространства, где полная энергия Е частицы меньше уровня потенциальной энергии. Туннельный эффект имеет квантовую природу и связан с наличием у частиц волновых свойств.
На рисунке представлена некоторая произвольная зависимость потенциальной энергии U от координаты х частицы в области одномерного потенциального барьера.
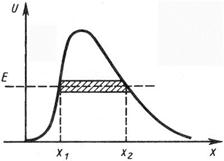
Коэффициентом прозрачности D потенциального барьера называется величина
,
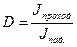где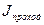 
– интенсивность волны де Бройля, прошедшей сквозь потенциальный барьер, 
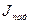– интенсивность волны, падающей на барьер.
Для прямоугольного потенциального барьера
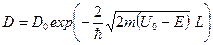, (1.8)
где m – масса частицы, Е – ее энергия, L – ширина барьера.
Для потенциального барьера произвольной формы (рисунок).
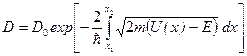. (1.9)
Согласно условию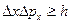 
неопределенности 
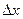координаты х частицы будет соответствовать неопределенность импульса частицы 
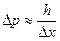, что не позволяет говорить об определенном значении кинетической энергии 
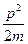частицы. Это значит, что неопределенность кинетической энергии частицы 
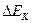, вызванная фиксированием её координаты, превышает разность между высотой потенциального барьера 
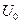и энергией Е частицы:
.
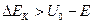Неопределенность кинетической энергии частицы устраняет парадокс отрицательности кинетической энергии частицы в области потенциального барьера.
