Вариация функционала

Опр.1 Отображение некоторого множества в множество действительных чисел называется функционалом, определенным на этом множестве.

Замечание Функционал – обобщение понятия функции.

Обозначают: 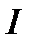- функционал; 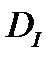- область определения; 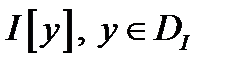- значение функционала на элементе .

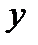Опр.2 Функционал 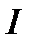достигает 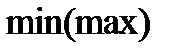на 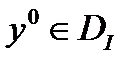, если 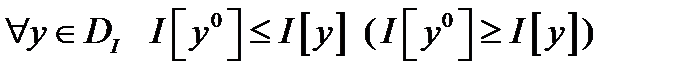. Обозначают: 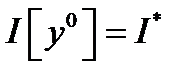. Вариационное исчисление изучает общие методы решения экстремальных задач, связанных с функционалами, определенными на множестве функций.

Определим 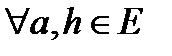(линейное пространство над полем действительных чисел) функцию .

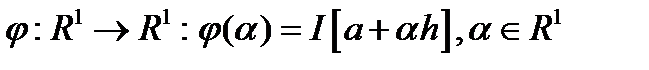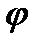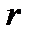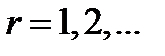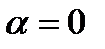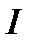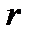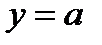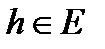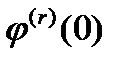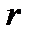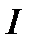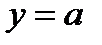Опр.3 Если дифференцируема раз () в точке , то говорят, что функционал дифференцируем раз в точке вдоль направления , а производную называют вариацией функционала в вдоль 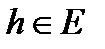и обозначают 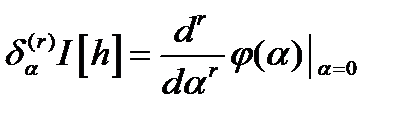. Если 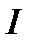дифференцируем 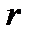раз в 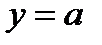вдоль 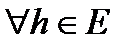, то говорят, что 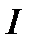имеет вариацию 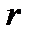порядка в точке .

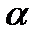Если 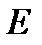линейное нормированное пространство, то для 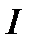можно ввести понятие локального экстремума:

Опр.4 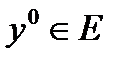называется точкой локального минимума функционала 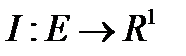, если 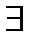окрестность 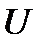точки 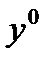, что .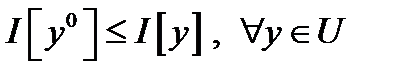

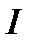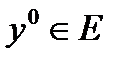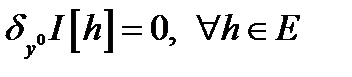Опр.5 Если имеет первую вариацию в и , то 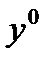- стационарная точка функционала .

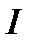Опр.6 Если 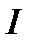имеет вторую вариацию в 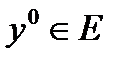и 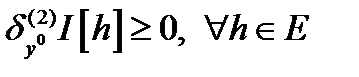, то вариация функционала 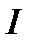положительна в .

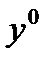Теорема 1. (необходимое условие локального экстремума): Если точка 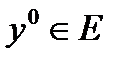- локальный минимум функционала 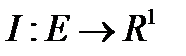, то:

1) если 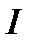имеет первую вариацию в 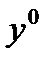, то 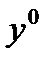- стационарная точка ;

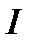2) если 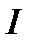имеет вторую вариацию в 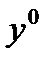, то она положительна.