Доказательство. Рассмотрим Выбором малого можно добиться, чтобы находился в сколь угодно малой окрестности

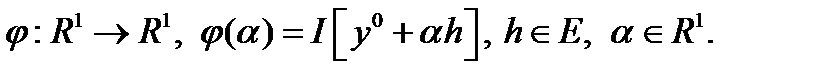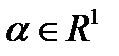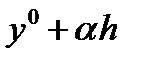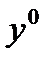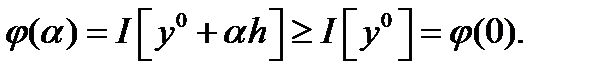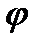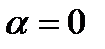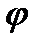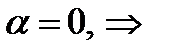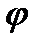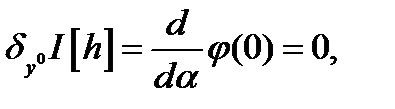
Рассмотрим Выбором малого можно добиться, чтобы находился в сколь угодно малой окрестности . Тогда (опр.4) справедливо Если выполнено 1), то дифференцируема в , а если выполнено 2), то дважды дифференцируема в (по свойствам локального минимума функции ) 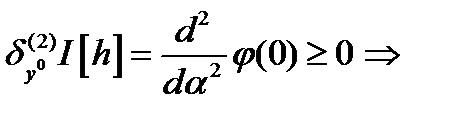т.к. 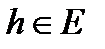произвольно и из предыдущего соотношения следует доказательство теоремы. ч.т.д.