Метод штрафных функций применяется для решения задач условной оптимизации и относится к методам последовательной безусловной минимизации. Основная идея метода заключается в сведении исходной задачи:
 (1)
(1) 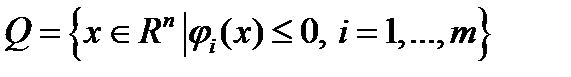 (2) к последовательности задач оптимизации
(2) к последовательности задач оптимизации
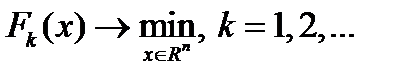 (3), где
(3), где  некоторая вспомогательная функция, которая подбирается так, чтобы с ростом номера
некоторая вспомогательная функция, которая подбирается так, чтобы с ростом номера  она мало отличалась от исходной функции
она мало отличалась от исходной функции  на множестве
на множестве  и быстро возрастала на множестве
и быстро возрастала на множестве 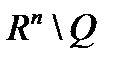 . Быстрый рост
. Быстрый рост  вне
вне 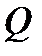 приводит к тому, что при больших
приводит к тому, что при больших  нижняя грань этой функции на
нижняя грань этой функции на 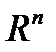 будет достигаться в точках, близких к множеству
будет достигаться в точках, близких к множеству 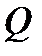 , и решения задачи (3) будет приближаться при определенных условиях к решению исходной задачи (1)-(2). При этом имеется достаточно большой произвол в выборе функций
, и решения задачи (3) будет приближаться при определенных условиях к решению исходной задачи (1)-(2). При этом имеется достаточно большой произвол в выборе функций  . Это позволяет подобрать наиболее удобный вид минимизируемой функции
. Это позволяет подобрать наиболее удобный вид минимизируемой функции  и применять более простые методы безусловной оптимизации.
и применять более простые методы безусловной оптимизации.
Опр. 1 Функция 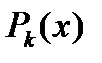 называется штрафной функцией множества
называется штрафной функцией множества 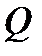 , если
, если 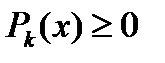 для любых
для любых 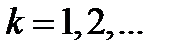 ,
,  и
и 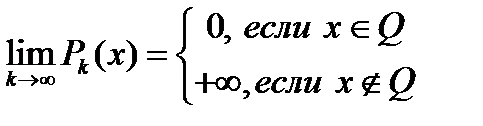
Из этого определения видно, что при больших  за нарушение условия
за нарушение условия 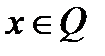 приходится платить большой штраф, в то время как при
приходится платить большой штраф, в то время как при 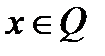 этот штраф стремится к нулю с ростом
этот штраф стремится к нулю с ростом  (рис.1).
(рис.1).
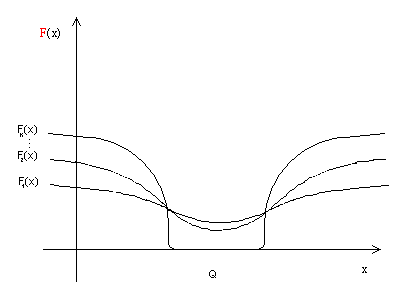
Рис.1 Штрафные функции
Для любого множества Q можно указать сколь угодно много штрафных функций. Пусть  и
и 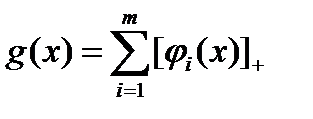 .Теперь множество допустимых решений представимо в виде:
.Теперь множество допустимых решений представимо в виде:  , и штрафными функциями являются, например, следующие:
, и штрафными функциями являются, например, следующие:
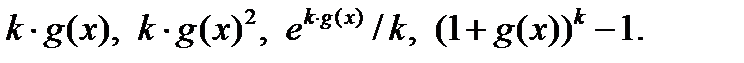
Пусть штрафная функция  уже выбрана. Положим
уже выбрана. Положим 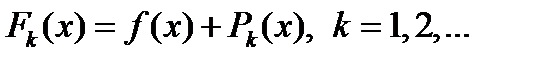 и будем считать, что
и будем считать, что 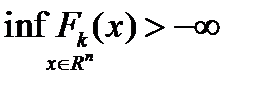 , для всех
, для всех  . (4)
. (4)
Тогда, для каждого k можно постараться найти решение задачи (3) и получить последовательность оптимальных решений. К сожалению, нижняя грань в (4) может достигаться не при всех k. Поэтому зададимся последовательностью  такой, что
такой, что  и
и 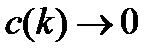 при
при  и с помощью какого-либо метода безусловной оптимизации найдем точки
и с помощью какого-либо метода безусловной оптимизации найдем точки 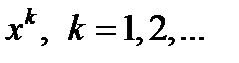 , удовлетворяющие условию
, удовлетворяющие условию 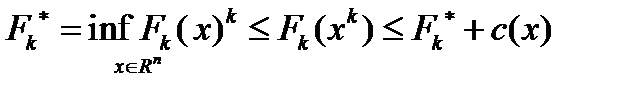 . (5)
. (5)
Другими словами, вместо точного решения  будем искать приближенное решение
будем искать приближенное решение 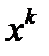 с погрешностью, не превышающей
с погрешностью, не превышающей 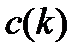 . Отметим, что, вообще говоря,
. Отметим, что, вообще говоря, 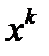 может не принадлежать Q. Дальнейшее изложение уже не зависит от того, каким именно методом найдена точка
может не принадлежать Q. Дальнейшее изложение уже не зависит от того, каким именно методом найдена точка 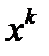 . Поэтому ограничимся предположением о существовании такого метода и перейдем к исследованию сходимости метода штрафных функций.
. Поэтому ограничимся предположением о существовании такого метода и перейдем к исследованию сходимости метода штрафных функций.
Пусть штрафные функции  задаются с помощью вспомогательных функций
задаются с помощью вспомогательных функций 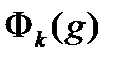 равенствами
равенствами  и
и 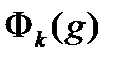 такова, что
такова, что
а) 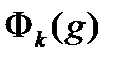 определены и непрерывны для всех
определены и непрерывны для всех  ;
;
б) 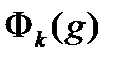 положительны, монотонно возрастают по
положительны, монотонно возрастают по 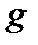 и
и 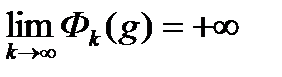 для
для 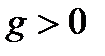 ;
;
с) 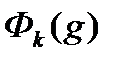 сходится к 0 равномерно при
сходится к 0 равномерно при 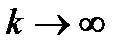 в области
в области 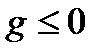 . Тогда следующая теорема дает достаточные условия сходимости метода штрафных функций.
. Тогда следующая теорема дает достаточные условия сходимости метода штрафных функций.
Теорема 1. Пусть функция f, g определены и непрерывны на 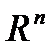 ,
, 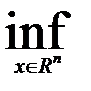
 , штрафные функции удовлетворяют условиям a), b), c) и последовательность
, штрафные функции удовлетворяют условиям a), b), c) и последовательность 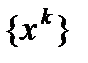 определяется соотношениями (5) (п.8.1). Тогда
определяется соотношениями (5) (п.8.1). Тогда
1) 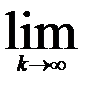
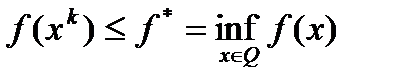 и
и 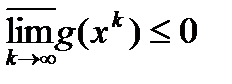 ; 2) если
; 2) если 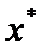 принадлежит множеству L
принадлежит множеству L 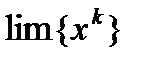 предельных точек последовательности
предельных точек последовательности 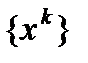 , то
, то  и
и 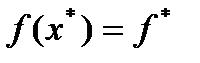 ; 3) если множество
; 3) если множество 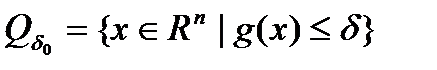 ограничено для некоторого
ограничено для некоторого 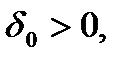 то
то  и
и 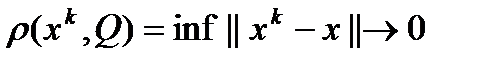 при
при 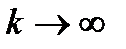 .
.
Доказательство.
1) По определению 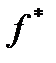 существует последовательность
существует последовательность 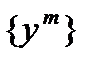 ,
, 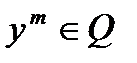 , для которой
, для которой 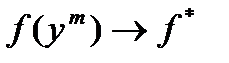 при
при  . Тогда для любого
. Тогда для любого 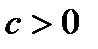 найдутся номера
найдутся номера 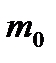 ,
, 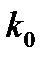 , такие, что
, такие, что 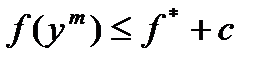 ,
, 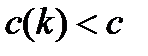 при
при 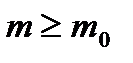 ,
, 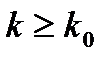 . Учитывая
. Учитывая 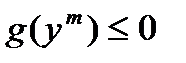 и условие с), можно считать, что
и условие с), можно считать, что  при
при 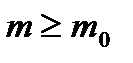 ,
, 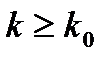 . Из этих неравенств и условий теоремы имеем
. Из этих неравенств и условий теоремы имеем 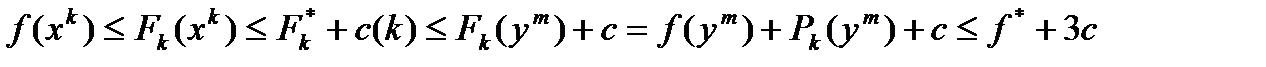 .
.
Следовательно, 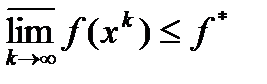 . Заметим, что при
. Заметим, что при 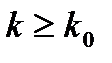 справедливо неравенство
справедливо неравенство 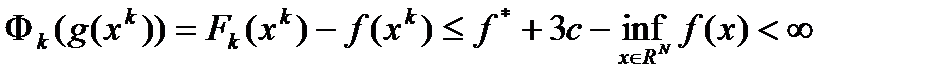 .Покажем, что отсюда следует неравенство
.Покажем, что отсюда следует неравенство 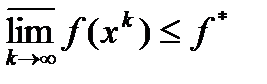 Предположим, что верно обратное неравенство. Тогда существует последовательность
Предположим, что верно обратное неравенство. Тогда существует последовательность 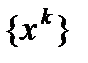 , для которой
, для которой 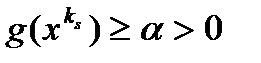 для всех s больших некоторого
для всех s больших некоторого 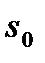 . Из условия b) имеем
. Из условия b) имеем 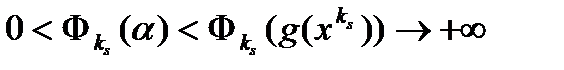 при
при 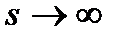 . Противоречие.
. Противоречие.
2) Пусть  . Тогда существует последовательность
. Тогда существует последовательность 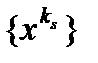 сходящаяся к
сходящаяся к 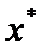 . Функция
. Функция  непрерывна и, как доказано раннее,
непрерывна и, как доказано раннее, 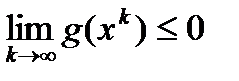 . Поэтому
. Поэтому 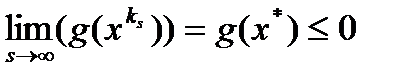 .
.
Следовательно, 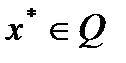 . Из условий теоремы имеем
. Из условий теоремы имеем 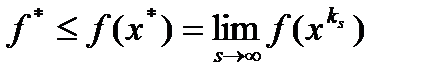 , а из определения верхнего предела следует обратное неравенство
, а из определения верхнего предела следует обратное неравенство 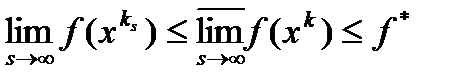 . Поэтому
. Поэтому  .
.
3) Докажем, что из установленного неравенства 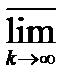
 следует
следует 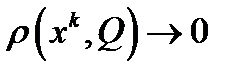 при
при 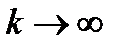 . Предположим, что существует
. Предположим, что существует  такое, что для любого
такое, что для любого 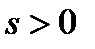 найдется номер
найдется номер  , для которого
, для которого 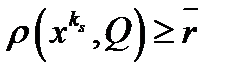 . Рассмотрим подпоследовательность
. Рассмотрим подпоследовательность  . Из условия
. Из условия 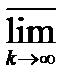
 следует, что существует номер
следует, что существует номер  такой, что для любого
такой, что для любого 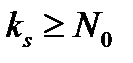 справедливо
справедливо 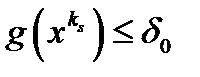 . Так как множество
. Так как множество 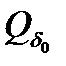 компактно, то без ограничения общности можно считать, что подпоследовательность
компактно, то без ограничения общности можно считать, что подпоследовательность  сходится к точке
сходится к точке  . Из непрерывности функции
. Из непрерывности функции 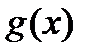 получим
получим  и следовательно,
и следовательно, 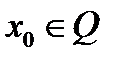 . Учитывая компактность множества
. Учитывая компактность множества 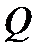 , с помощью неравенства треугольника легко доказать, что для любых точек
, с помощью неравенства треугольника легко доказать, что для любых точек 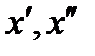 справедливо неравенство
справедливо неравенство 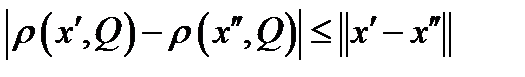 .Следовательно, функция
.Следовательно, функция  непрерывна. Тогда
непрерывна. Тогда  .Поэтому справедливо неравенство
.Поэтому справедливо неравенство 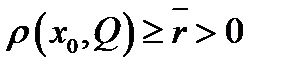 . В то же время выше доказано, что
. В то же время выше доказано, что 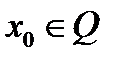 . Получаем противоречие. Показано, что из неравенства
. Получаем противоречие. Показано, что из неравенства 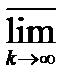
 следует
следует 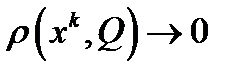 при
при 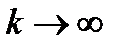 . Аналогичным образом можно показать, что из неравенства
. Аналогичным образом можно показать, что из неравенства 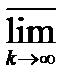
 следует
следует  . ч.т.д.
. ч.т.д.
Заметим, что метод штрафных функций в некотором смысле близок к методу множителей Лагранжа. В самом деле, при составлении функции Лагранжа ограничения задачи заносятся в целевую функцию с неизвестными множителями, что можно рассматривать как штраф за нарушение соответствующих ограничений. Достоинством метода множителей Лагранжа является то, что в нем отсутствуют неограниченно растущие коэффициенты типа штрафных коэффициентов. В то же время метод множителей Лагранжа предполагает существование седловой точки, а метод штрафных функций может использоваться для более широких классов задач и является более универсальным.
 2015-01-21
2015-01-21 1377
1377
