2015-01-21
514
Лемма 1 (Дюбуа-Реймона) Для выполнения соотношения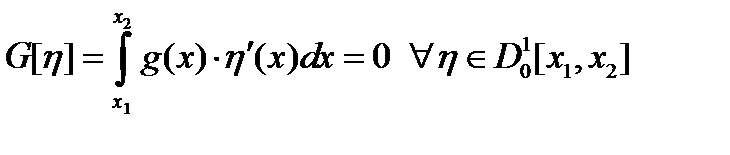 
(1) при некоторой функции 
.
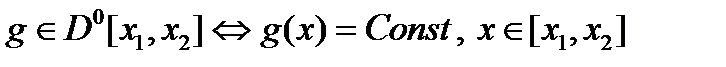Лемма 2. Для выполнения соотношения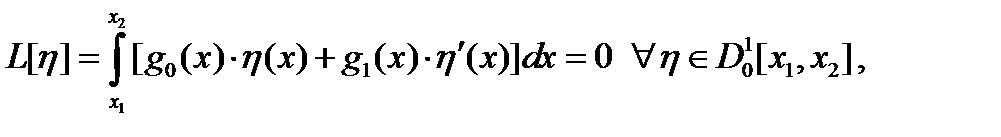 
(2) при некоторых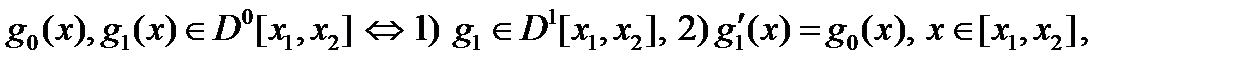 
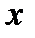- точки непрерывности функции 
.
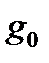Опр.1 Функция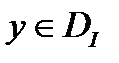 
удовлетворяет интегро-дифференциальному уравнению Эйлера-Лагранжа, отвечающего основной функции 
, если 
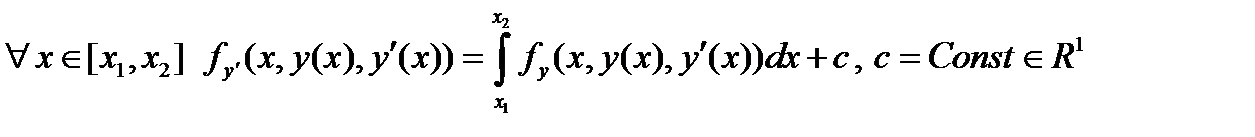. (3)
Теорема 1. Если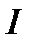 
достигает на 
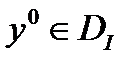локального (слабого) минимума и 
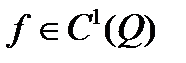, то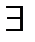 
константа 
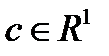, что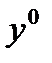 
удовлетворяет интегро-дифференциальному уравнению Эйлера-Лагранжа.
Док-во:
Пусть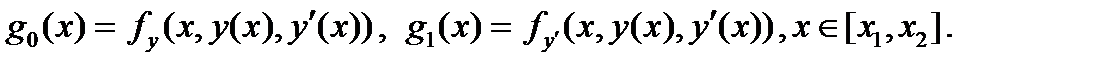 
Справедливость доказываемой теоремы вытекает из (Т 1, п. 10.2) и леммы2.
Замечание. Если в (3)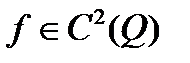 
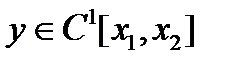, то (3) можно продифференцировать по 
: 
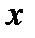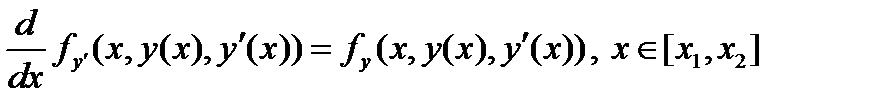(4)
Опр.2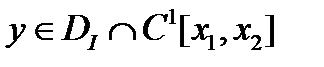 
удовлетворяет дифференциальному уравнению Эйлера-Лагранжа (4), отвечающему 
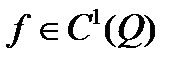, если эта функция обращает (4) в тождество.
Теорема 2. Пусть в задаче 1 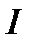достигает на 
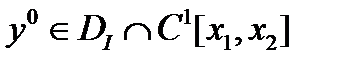локального (слабого) минимума и 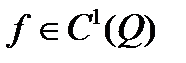. Тогда 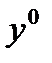удовлетворяет (4).
Теорема 2 является следствием теоремы 1.
Теорема 3 (Необходимые условия локального минимума 2 порядка). Если в задаче 1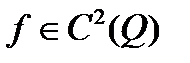 
, в 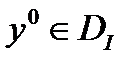существует вторая вариация функционала , а он сам достигает в нем локального минимума, то вторая вариация функционала в 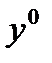положительна на 
.
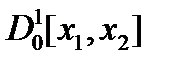Док-во:
Справедливость Т3 следует из (утверждения 2) Т.1 п. 10.1) и того, что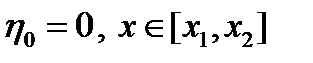 
доставляет локальный минимум 
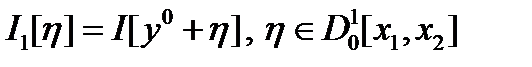. Введем обозначения: для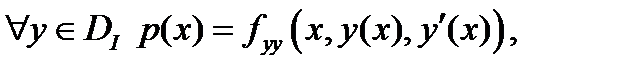 
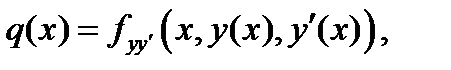
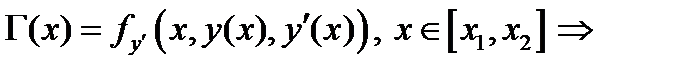
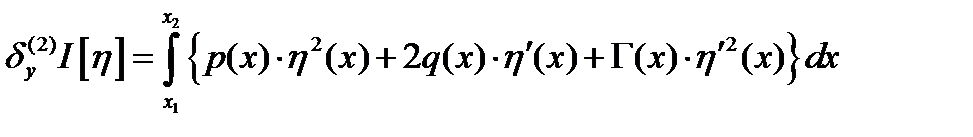
20. Условия Лежандра и Якоби
Опр.1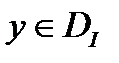 
удовлетворяет условию Лежандра, если 
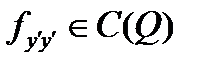и имеет место неравенство 
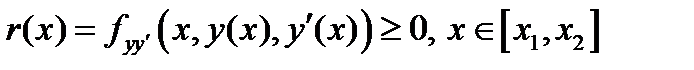. (1)
Если (1) строгое, то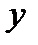 
удовлетворяет сильным условиям Лежандра.
Теорема 1. Есл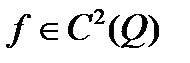и 
и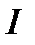 
достигает на 
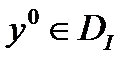локального (слабого) минимума, то 
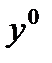удовлетворяет условию Лежандра.
