Представленные ниже алгоритмы предназначены для поиска экстремума при наличии ограничений только типа неравенств.
Рассмотрим задачу min f(x) (1), 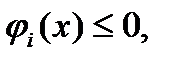
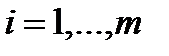 (2),
(2), 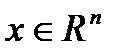 (3), где f(x),
(3), где f(x), 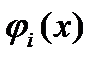 выпуклые функции. Вводя дополнительные переменную и ограничение, можно сделать функционал задачи линейным: min y (4),
выпуклые функции. Вводя дополнительные переменную и ограничение, можно сделать функционал задачи линейным: min y (4), 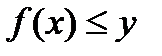 (5),
(5), 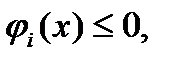
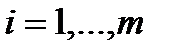 (6),
(6), 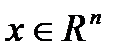 (7)
(7)
Поэтому без ограничения общности будем считать, что 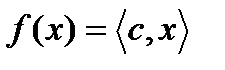 .Пусть, как и прежде,
.Пусть, как и прежде, 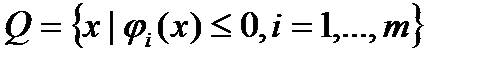 множество допустимых решений задачи (1)-(3),
множество допустимых решений задачи (1)-(3), 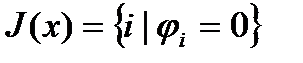 , и выполняется условие Слейтеда.
, и выполняется условие Слейтеда.
Ненулевой вектор p назовем возможным направлением для множества Q из точки x, если найдется 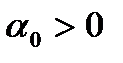 такое, что для всех
такое, что для всех 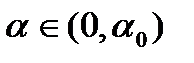 точка
точка 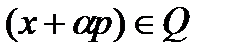 .
.
Ненулевой вектор p называется направлением спуска для множества Q из точки x, если p возможное направление из этой точки и 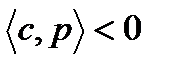 .
.
Для фиксированной точки 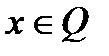 рассмотрим вспомогательную задачу линейного программирования
рассмотрим вспомогательную задачу линейного программирования  (8),
(8), 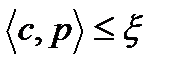 (9),
(9), 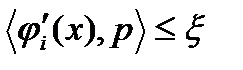 для всех
для всех 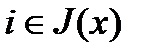 (10),
(10), 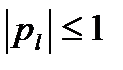 , для всех
, для всех 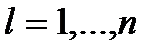 . (11) Условие (11) называется условиями нормировки. Из условий (11) и (9) следует, что целевая функция (8) ограничена снизу на множестве допустимых решений. Тогда из критерия разрешимости для задачи линейного программирования следует, что найдется хотя бы одно оптимальное решение
. (11) Условие (11) называется условиями нормировки. Из условий (11) и (9) следует, что целевая функция (8) ограничена снизу на множестве допустимых решений. Тогда из критерия разрешимости для задачи линейного программирования следует, что найдется хотя бы одно оптимальное решение 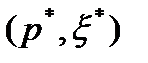 задачи (8)-(11). Нулевое решение
задачи (8)-(11). Нулевое решение  является допустимым решением вспомогательной задачи и, значит,
является допустимым решением вспомогательной задачи и, значит, 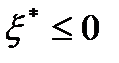 .
.
Предположим, что 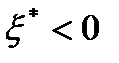 . Тогда
. Тогда 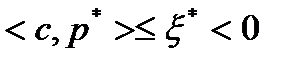 и
и 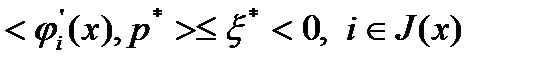 . Следовательно,
. Следовательно, 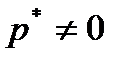 и для любого номера
и для любого номера 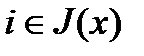 имеем
имеем  для всех достаточно малых
для всех достаточно малых 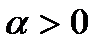 . Если
. Если 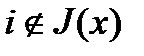 , то есть
, то есть 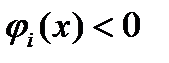 , то в силу непрерывности функции
, то в силу непрерывности функции 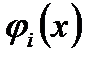 неравенство
неравенство 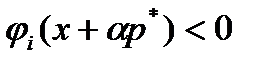 будет выполняться для всех достаточно малых
будет выполняться для всех достаточно малых 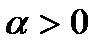 . Поэтому найдется
. Поэтому найдется 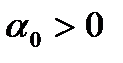 такое, что
такое, что 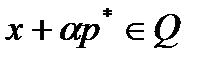 для всех
для всех 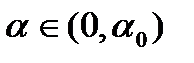 , и, следовательно, вектор
, и, следовательно, вектор 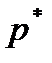 является возможным направлением для множества
является возможным направлением для множества 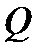 из точки
из точки 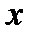 . Из неравенства (9) получим, что
. Из неравенства (9) получим, что 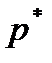 является также и направлением спуска. Следовательно,
является также и направлением спуска. Следовательно,  . Если
. Если 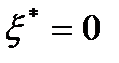 , то нельзя утверждать, что
, то нельзя утверждать, что 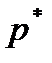 будет возможным направлением спуска или направлением спуска в точке
будет возможным направлением спуска или направлением спуска в точке 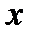 . Например, может оказаться, что
. Например, может оказаться, что 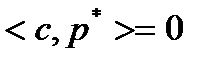 или
или 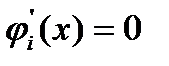 для некоторого номера
для некоторого номера 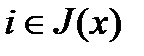 .
.
В случае общей задачи нелинейного программирования без дополнительных условий типа выпуклости равенство 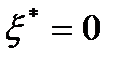 является лишь необходимым условием минимума. Для задачи выпуклого программирования (1), (3) при выполнении условия Слейтера последнее равенство является также достаточным условием оптимальности.
является лишь необходимым условием минимума. Для задачи выпуклого программирования (1), (3) при выполнении условия Слейтера последнее равенство является также достаточным условием оптимальности.
Теорема 1(критерий оптимальности)
Пусть 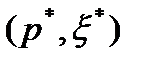 оптимальное решение вспомогательной задачи для
оптимальное решение вспомогательной задачи для 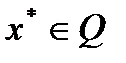 . Тогда
. Тогда 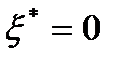 в том и только том случае, когда
в том и только том случае, когда 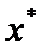 - оптимальное решение задачи (1)-(3).
- оптимальное решение задачи (1)-(3).
 2015-01-21
2015-01-21 400
400








