Пусть в простейшей вариационной задаче точки A и B находятся на кривых 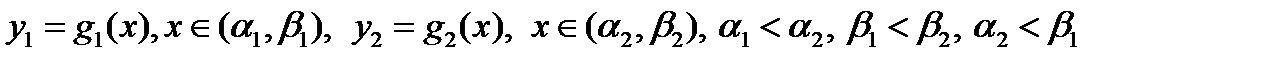 (1)
(1) 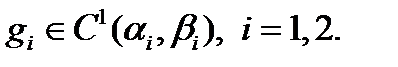
Функция y допустима, если удовлетворяет условиям допустимости в простейшей вариационной задаче, а граничные точки выбираются произвольно на кривых, определяемых (1). Минимизируемый функционал имеет нефиксированные пределы интегрирования.
Рассмотрим задачу: 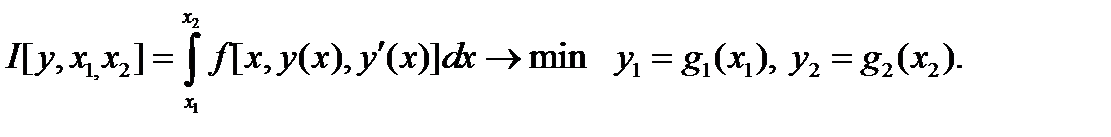
Рассмотрим сначала случай 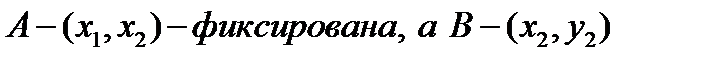 удовлетворяет уравнению:
удовлетворяет уравнению: 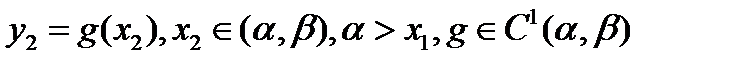 . Функционал обозначим:
. Функционал обозначим: 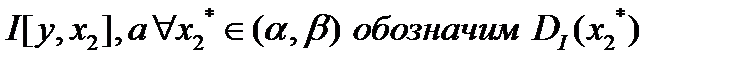 - класс допустимых функций в простейшей задаче вариационного исчисления, в которой
- класс допустимых функций в простейшей задаче вариационного исчисления, в которой 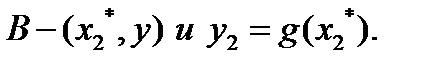
Теорема 1. Если 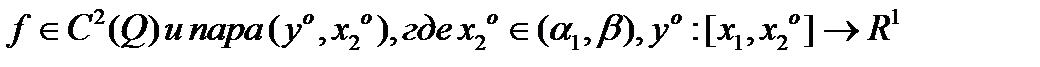 - решение задачи с подвижным правым концом, то необходимо
- решение задачи с подвижным правым концом, то необходимо 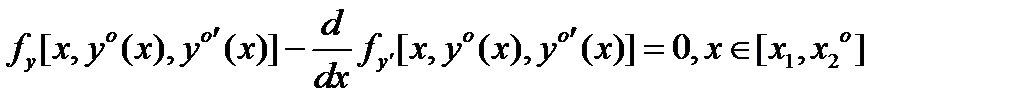 (2)
(2)
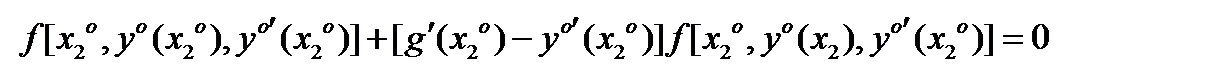 (3)
(3)
Доказательство:
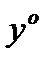 -решение простейшей задачи для
-решение простейшей задачи для  и (2) имеет место. Пусть
и (2) имеет место. Пусть 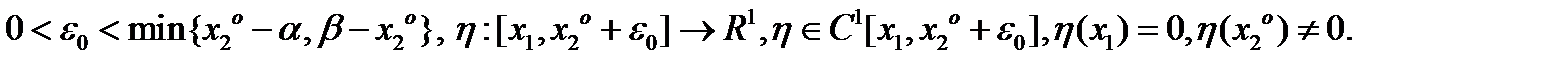
Т.к. 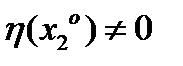 , то
, то 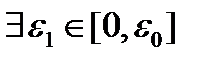 , что
, что 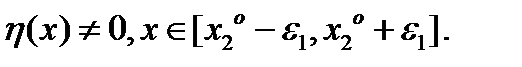 Пусть
Пусть 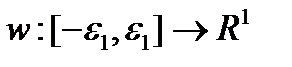 такая, что
такая, что 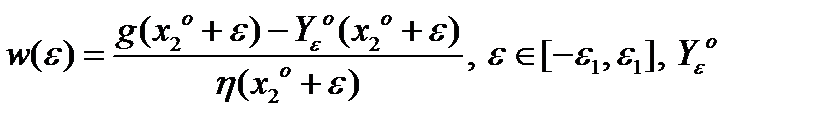 - непрерывно дифференцируемое расширение
- непрерывно дифференцируемое расширение  на
на 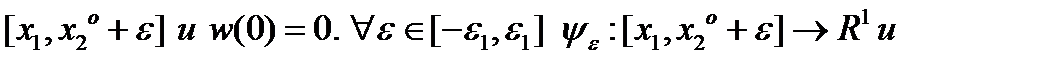
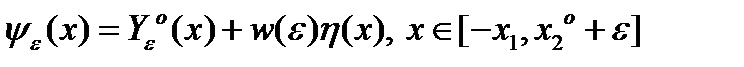 принадлежит
принадлежит 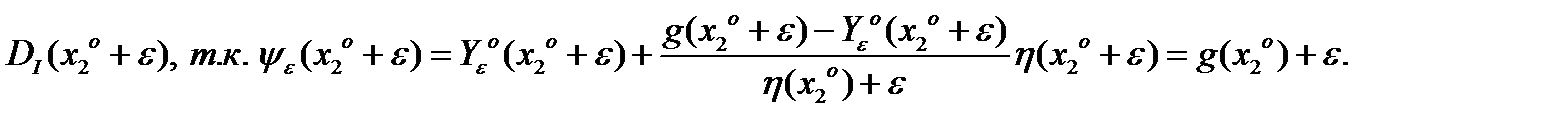
Положим 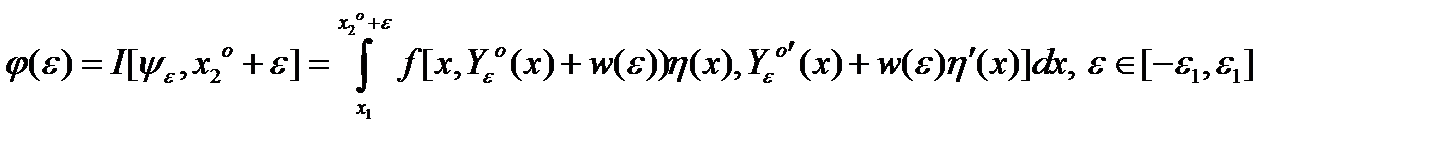
Т.к. 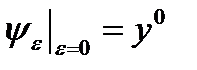 , то
, то 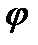 в
в 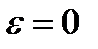 достигает локального минимума и
достигает локального минимума и 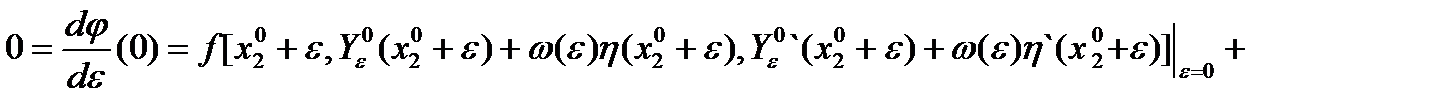
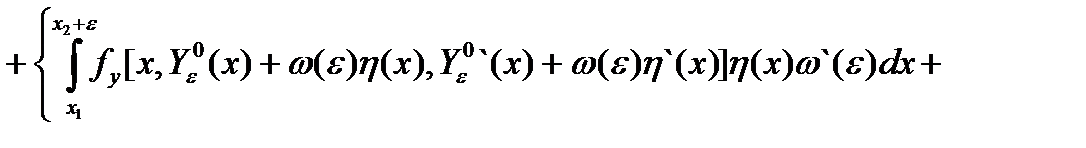
+ 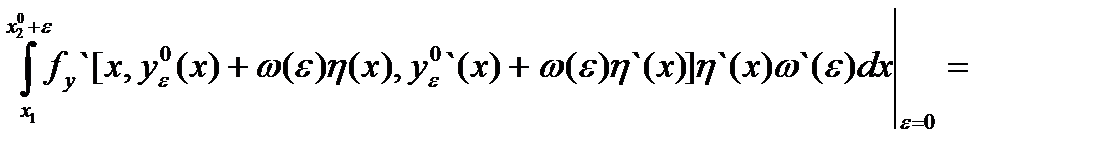 (4)
(4)
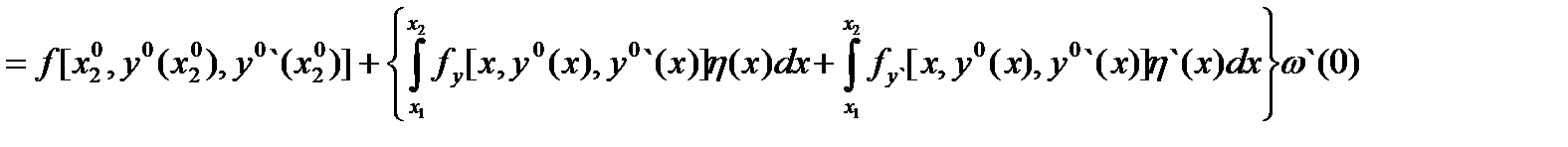 .
.
Т.к. 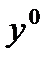 удовлетворяет дифференциальному уравнению Эйлера-Лагранжа, отвечающему основной функции
удовлетворяет дифференциальному уравнению Эйлера-Лагранжа, отвечающему основной функции 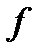 , то
, то
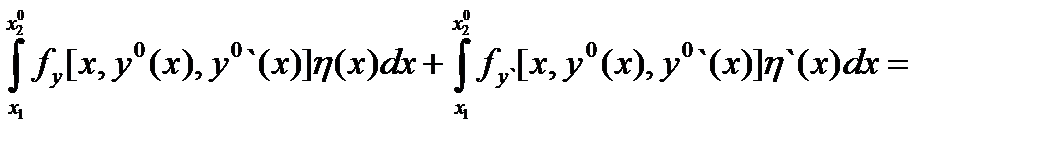
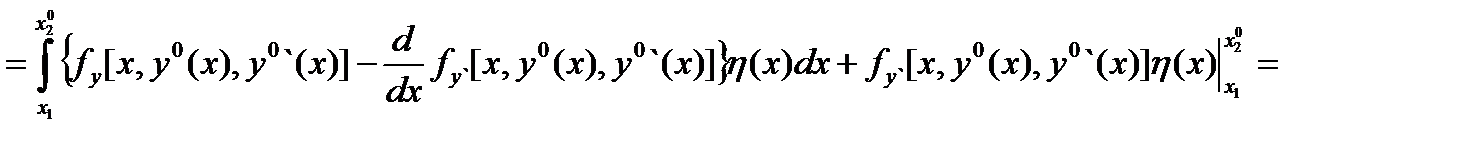
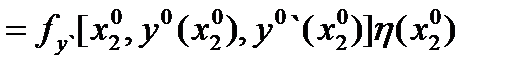 (5)
(5)
А 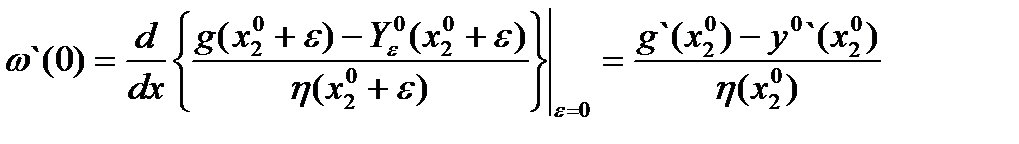 (6)
(6)
Преобразуя (4) с учетом (5) и (6), получаем
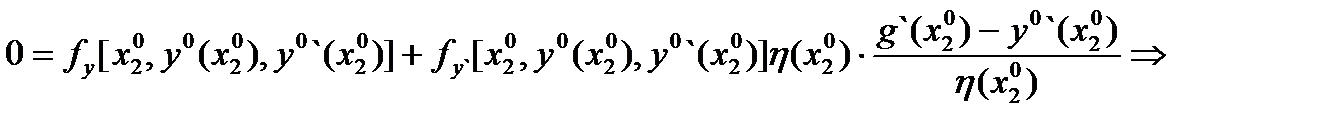
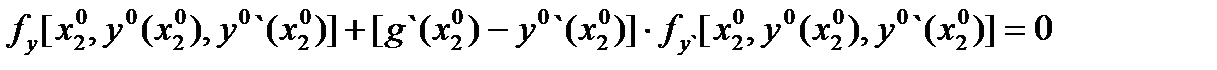
Равенство (3) называют условием трансверсальности на правом конце. Если правая кривая (граница) имеет уравнение 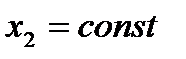 ,
, 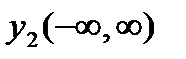 , то оно принимает вид
, то оно принимает вид 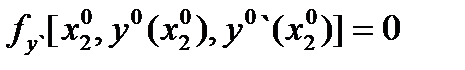
Аналогично можно рассмотреть случай незакрепленного левого конца или обоих концов.
 2015-01-21
2015-01-21 503
503








