На множестве допустимых функций накладывается условие: функционал, заданный на множестве допустимых функций (как и минимизируемый) должен принимать фиксированное значение на любой допустимой функции.
Пусть 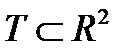 - открытое выпуклое множество,
- открытое выпуклое множество, 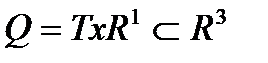 ,
, 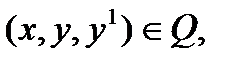
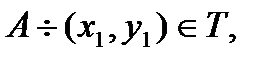
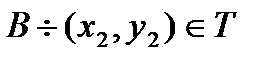 ,
, 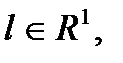
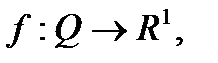
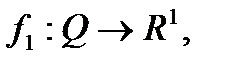
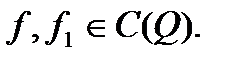 Функцию
Функцию 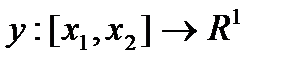 назовем допустимой
назовем допустимой 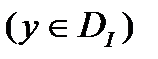 , если
, если 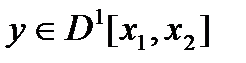 ,
, 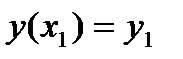 ,
, 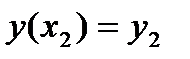 ,
, 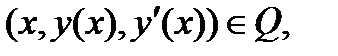
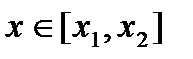 ,
, 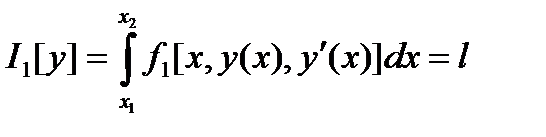 . Каждой
. Каждой 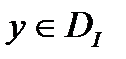 поставим в соответствие число
поставим в соответствие число 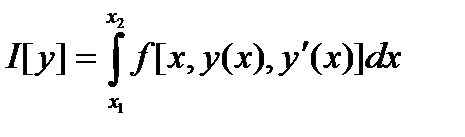 . Требуется минимизировать функционал I на
. Требуется минимизировать функционал I на 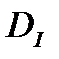 . В случае
. В случае 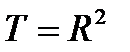 изопериметрическая задача имеет вид:
изопериметрическая задача имеет вид: 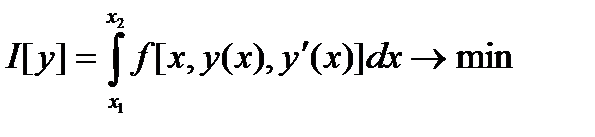 .
.
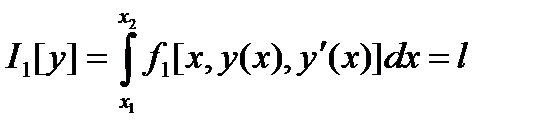 ,
, 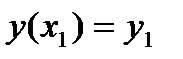 ,
, 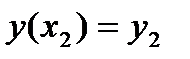 .Пусть
.Пусть 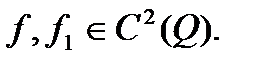 Для
Для 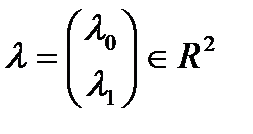 рассмотрим функционал
рассмотрим функционал 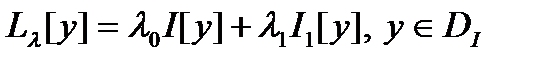 .
.
Теорема 1. Если 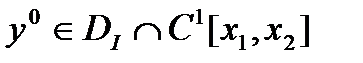 решение изопериметрической задачи, то найдется
решение изопериметрической задачи, то найдется 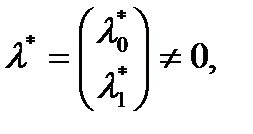 что
что 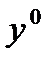 удовлетворяет уравнению Эйлера-Лагранжа, соответствующему функционалу
удовлетворяет уравнению Эйлера-Лагранжа, соответствующему функционалу 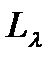 , т.е.
, т.е. 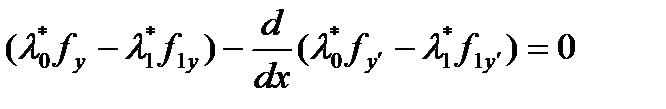 .
.
Доказательство. 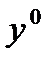 не стационарная функция для
не стационарная функция для 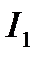 (иначе
(иначе 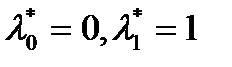 ). Пусть
). Пусть 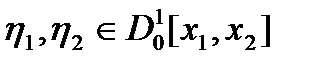 ,
, 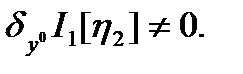 Такая
Такая 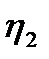 найдется, т.е.
найдется, т.е. 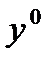 не стационарная для
не стационарная для 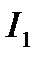 . Рассмотрим двухпараметрическое семейство функций
. Рассмотрим двухпараметрическое семейство функций
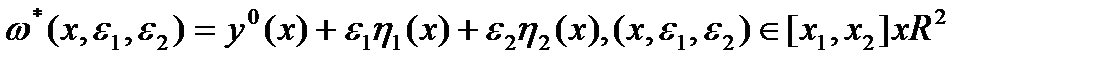 Причем
Причем 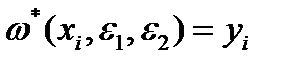 , i=1,2,
, i=1,2, 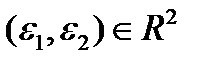 . Для малых по абсолютной величине
. Для малых по абсолютной величине 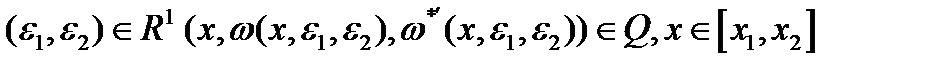 . Положим
. Положим 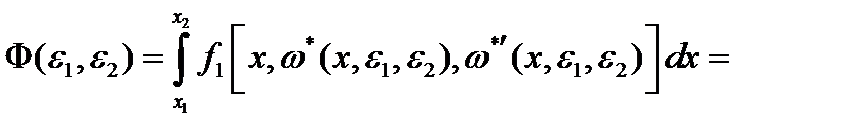
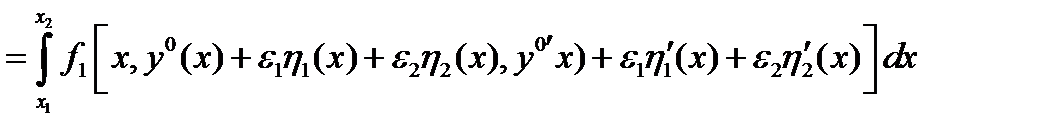 . Видно что
. Видно что 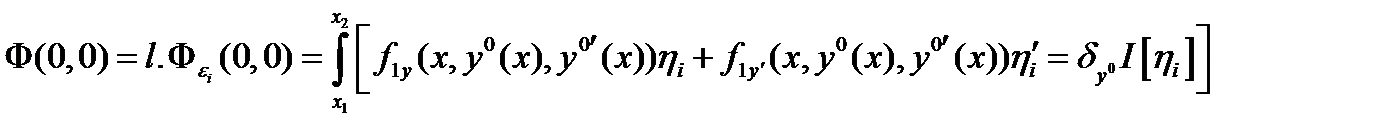 , i=1,2.
, i=1,2. 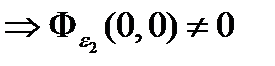 и по теореме о неявной функции уравнение
и по теореме о неявной функции уравнение 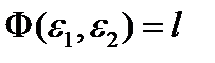 определяет функцию
определяет функцию 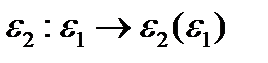 в окрестности точки
в окрестности точки 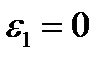 . При этом
. При этом 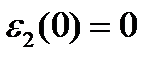 .
. 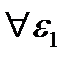 из малой окрестности О
из малой окрестности О 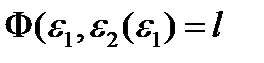 (1) и дифференцируя обе части (1) по
(1) и дифференцируя обе части (1) по 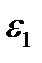 получаем
получаем 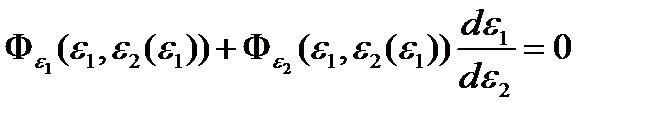 (2). Откуда с учетом
(2). Откуда с учетом 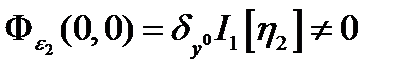 получаем
получаем 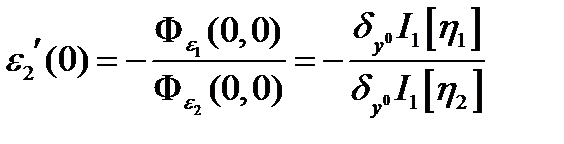 (3)
(3)
Рассмотрим однопараметрическое семейство функций
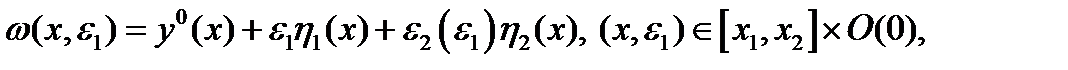 где
где 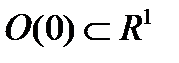 малая окрестность нуля. Из
малая окрестность нуля. Из 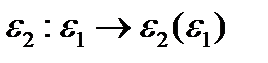 следует
следует 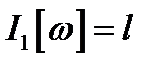 , что значит
, что значит 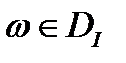 , а
, а 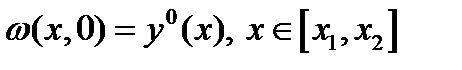 и
и 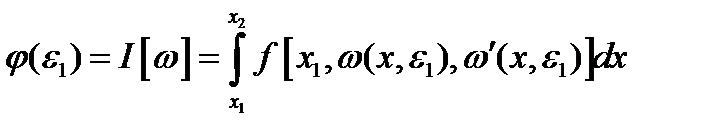 достигает минимума при
достигает минимума при 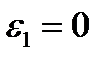 . Тогда
. Тогда 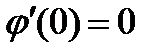 и с учетом (3) получаем
и с учетом (3) получаем 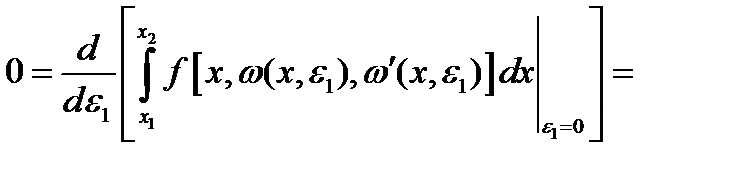
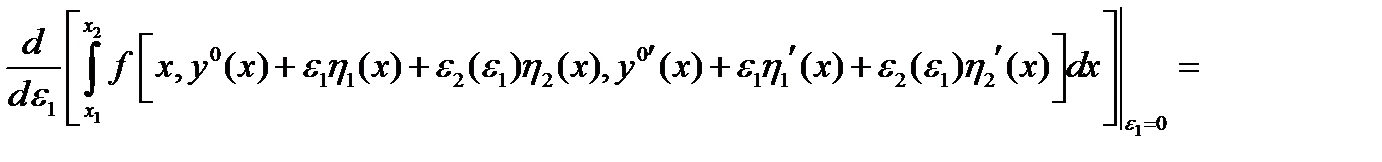 (4)
(4)
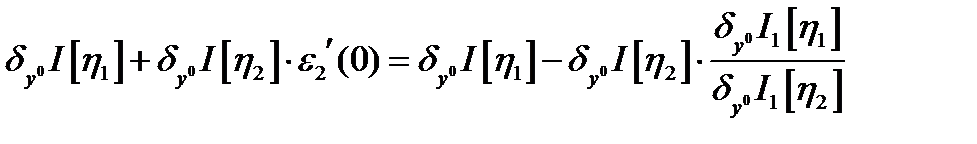 . Пусть
. Пусть 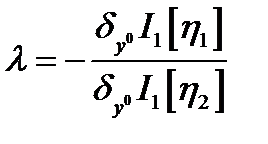 , тогда из (4)
, тогда из (4) 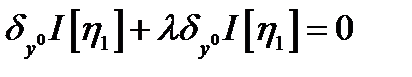 , что означает
, что означает 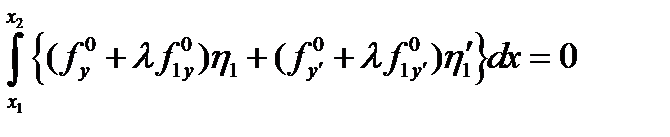 и интегрируя по частям получаем
и интегрируя по частям получаем 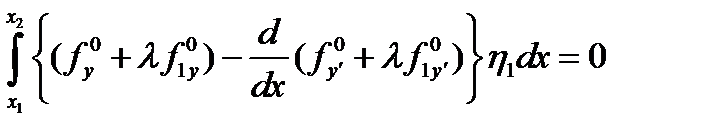 , при
, при 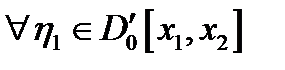 (5). Тогда из леммы Лагранжа
(5). Тогда из леммы Лагранжа 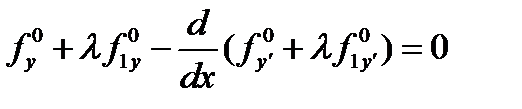 .
.
Замечание: интегральные кривые уравнения Эйлера-Лагранжа называют экстремалями. Экстремум может достигаться только на них. Из Т.1, если 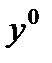 не экстремаль для
не экстремаль для 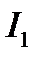 , то можно сразу взять
, то можно сразу взять 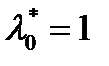 .
.
 2015-01-21
2015-01-21 433
433








