Доказательство. От противного приходим к 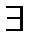точки и чисел , таких, что

От противного приходим к точки 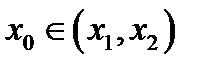и чисел 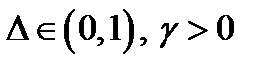, таких, что 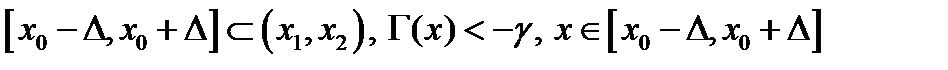. Определим последовательность функций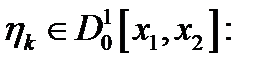

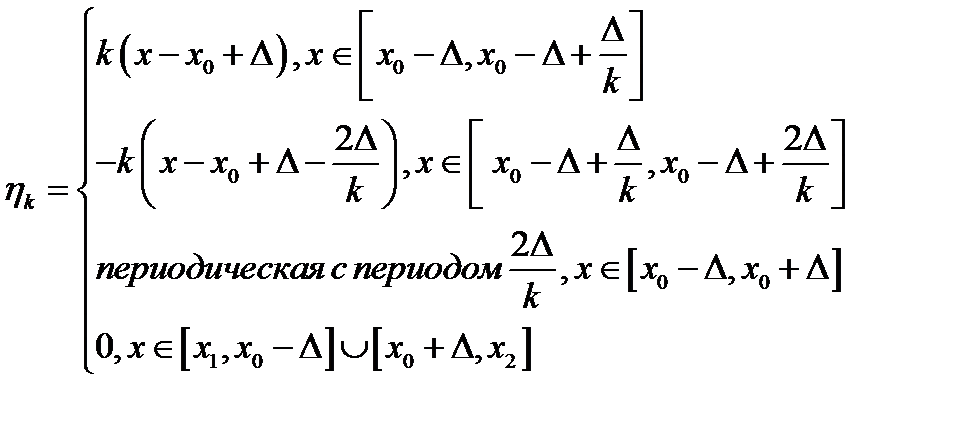
Для всех 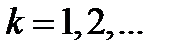справедливо 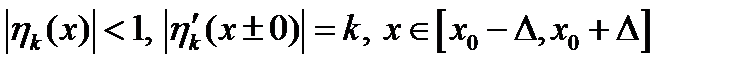. Вторая вариация функционала в 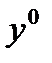вдоль

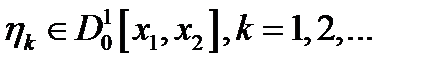
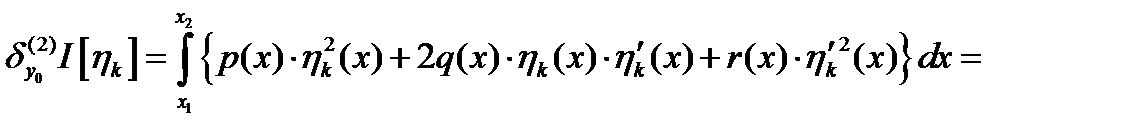
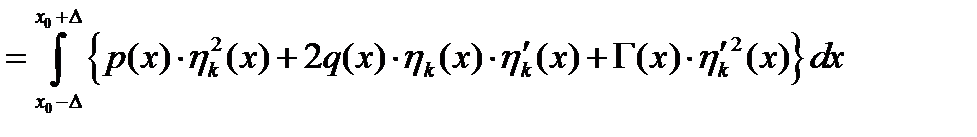(2)

Из (2) 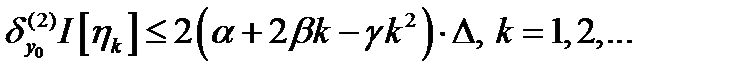(3) где 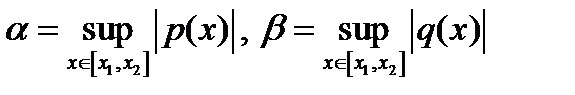и при 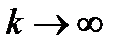правая часть (3) стремится к 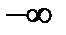и для больших 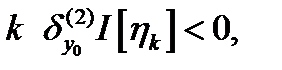что противоречит [Т.3, п.10.3]. ч.т.д.

Опр.2 Функция 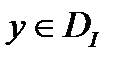удовлетворяет условию Якоби, если для нее выполнены сильное условие Лежандра и 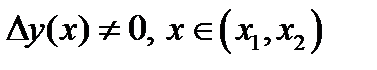, где 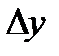- решение дифференциального уравнения Якоби (4) с начальными условиями 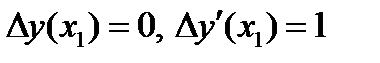. Если кроме того 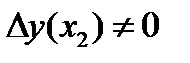, то будем говорить, что имеют место сильные условия Якоби.

Замечание. Если 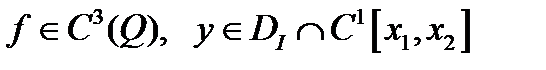удовлетворяет сильным условиям Лежандра, то уравнение Эйлера-Лагранжа, связанное с функционалом 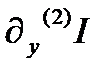называют дифференциальным уравнением Якоби, связанным с функционалом I и функцией у. Используя принятые выше обозначения оно имеет вид 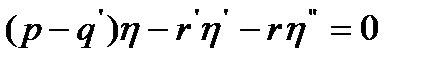(4)

Теорема 2. Пусть 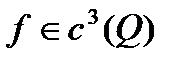, функция 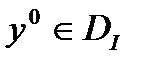доставляет локальный минимум (слабый) функционалу I и для нее выполняются сильные условия Лежандра. Тогда 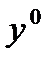удовлетворяет условиям Якоби.