Метод Ритца

Идея метода Ритца заключается в том, что значения некоторого функционала (например: 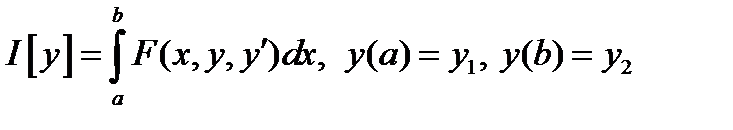) (1) рассматривается не на произвольных допустимых кривых вариационной задачи, а лишь на всевозможных линейных комбинациях вида 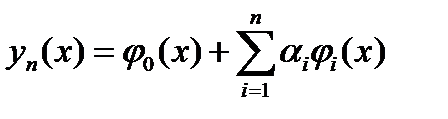(2) с постоянными коэффициентами, где 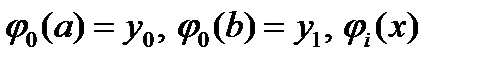- последовательность выбранных линейно независимых функций, причем 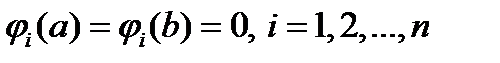. Эти функции называются координатными и 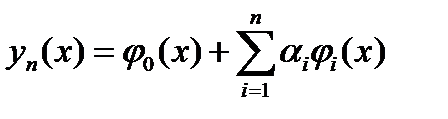должны быть допустимыми в рассматриваемой задаче, что налагает некоторые ограничения на выбор последовательности (2).

На функциях вида (2) функционал превращается в функцию от n переменных 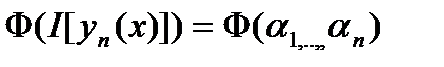коэффициентов 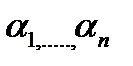. Эти коэффициенты выбираются так, чтобы 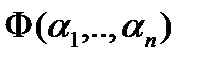достигала экстремума, т.е. определяются из соотношения 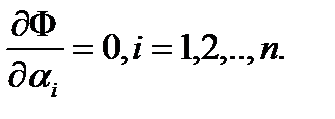(3). При найденных из системы (3) значениях 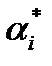, i=1,2,..,n приближённое решение вариационной задачи запишется в виде 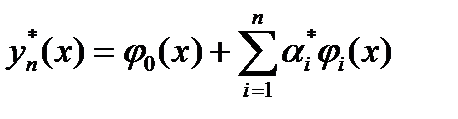(4). Если совершить предельный переход при 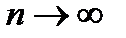, то получим в случае существования предела функцию 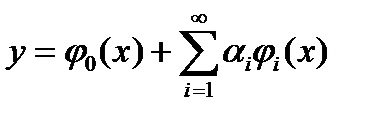, являющуюся точным решением рассматриваемой вариационной задачи. Если задача решается на определения абсолютного максимума, то значения находятся с избытком, т.к. минимум функционала на любых допустимых функциях не больше, чем на части этого класса функций.

Координатные функции должны быть допустимыми, и следовательно, прежде всего удовлетворять граничным условиям (не забывая и о других, например, гладкость, непрерывность). В случае 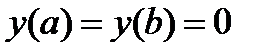в качестве координатных можно выбрать 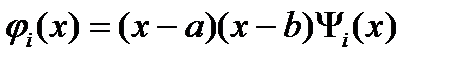, где 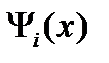какие-нибудь непрерывные функции, или

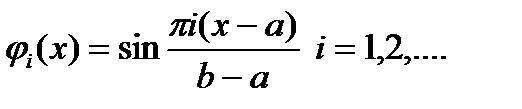, или какие-нибудь другие функции, удовлетворяющие условию 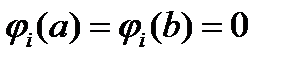. В случае неоднородных условий в качестве 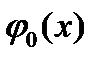можно выбрать 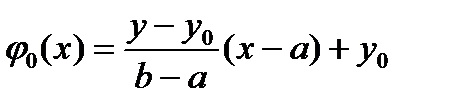, а остальные 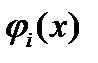выбираются из условий однородности, как отмечено выше. Условия сходимости последовательности 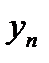, полученной методом Ритца, к решению вариационной задачи и оценки быстроты сходимости для конкретных, часто встречающихся задач разработаны в трудах Н.М. Крылова и Н.Н. Боголюбова. Например, для функционалов

вида 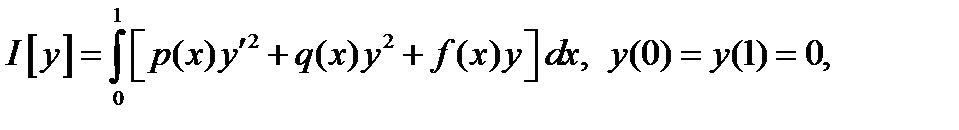где 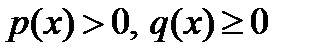не только доказана сходимость приближений, полученных по методу Ритца, к функции 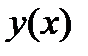, реализующей минимум функционала, при координатных функциях 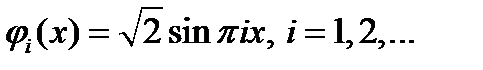, но и даны весьма точные оценки погрешности 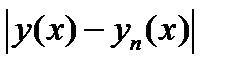. Например, весьма удобная оценка максимума 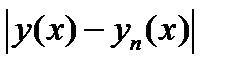на отрезке :

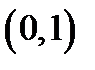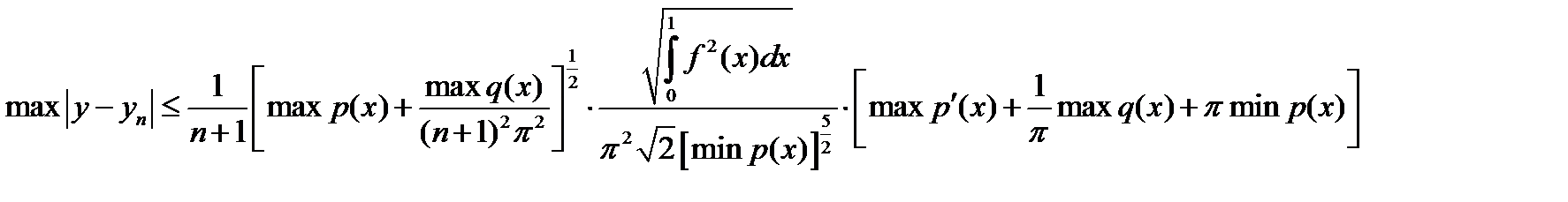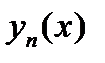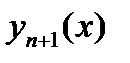и как видно, далее в простом случае оценка погрешности сложна. Поэтому для оценки точности результатов, полученных методом Ритца или другими прямыми методами обычно пользуются на практике следующим приемом: вычислив и сравнивают их между собой на отрезке 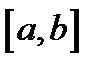в нескольких точках. Если требуемая точность достигнута, то считают, что решение вариационной задачи равно 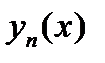. Иначе вычисляют 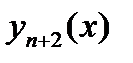и сравнивают с 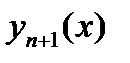в нескольких точках. Процесс продолжается, пока 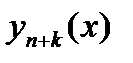и 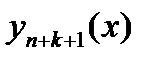не совпадут в пределах требуемой точности.

Замечание. Для приближенного решения вариационных задач, когда функционал зависит от нескольких переменных вместо метода Ритца обычно применяют метод Канторовича.