Рассмотрим случай, когда условия связи в вариационных задачах имеют вид функциональной зависимости.
Пусть 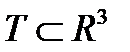 - открытое выпуклое множество,
- открытое выпуклое множество, 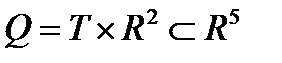 ,
, 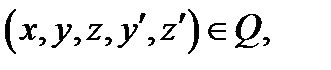
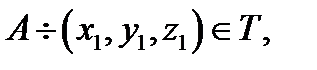
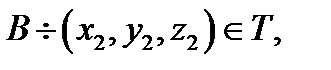
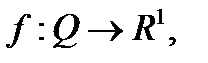
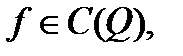
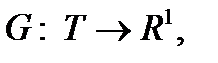
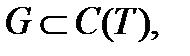
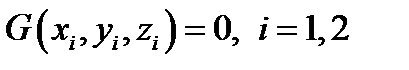 .
.
Вектор-функцию 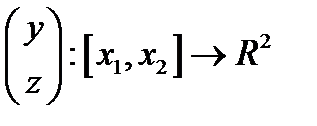 назовем допустимой,
назовем допустимой, 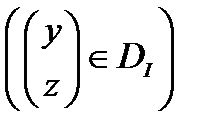 , если
, если 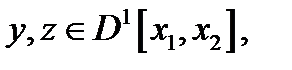
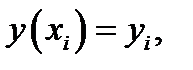
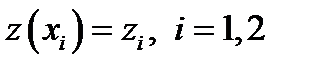 ,
, 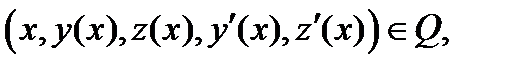
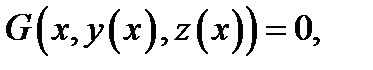
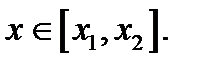 (1)
(1)
Каждой вектор-функции 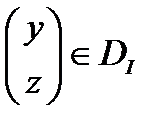 поставим в соответствие число по формуле
поставим в соответствие число по формуле 
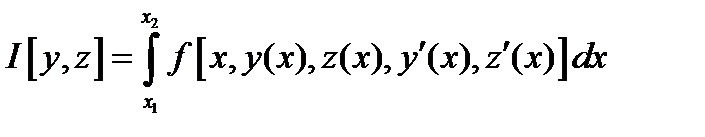
Требуется минимизировать приведенный функционал на 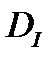 . Сформулированная задача носит название задачи Лагранжа с одной голономной связью (в условии связи нет производной от допустимой функции). При
. Сформулированная задача носит название задачи Лагранжа с одной голономной связью (в условии связи нет производной от допустимой функции). При 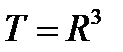 задача Лагранжа имеет вид:
задача Лагранжа имеет вид: 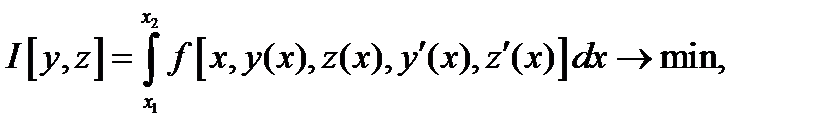
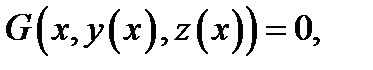
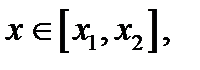
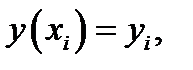
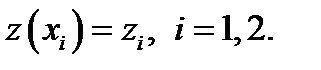
При выводе необходимых условий для 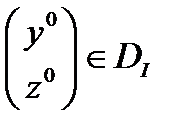 , предположим, что
, предположим, что 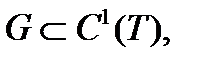
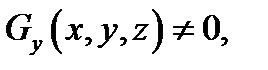
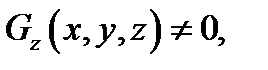 если
если 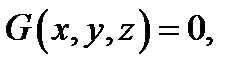

Теорема 1. Пусть 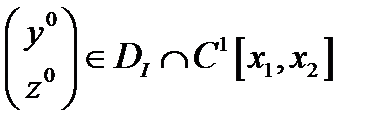 является решением задачи Лагранжа с одной голономной связью. Тогда найдется функция
является решением задачи Лагранжа с одной голономной связью. Тогда найдется функция 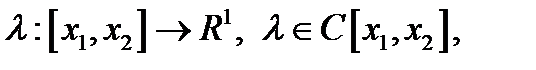 что будут выполняться равенства
что будут выполняться равенства 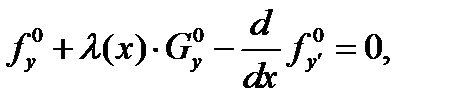
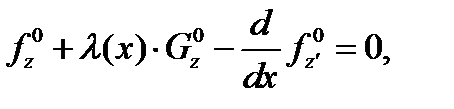 (2)
(2)
Если в уравнение связи входят и производные допустимых функций, то задача Лагранжа называется задачей с неголономной связью.
Опр.1 Проекцией множества А 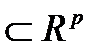 на координаты с номерами
на координаты с номерами 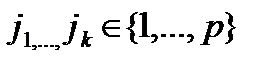 называется множество
называется множество 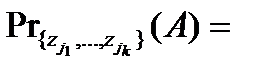
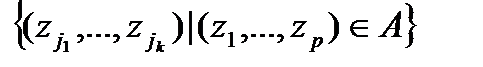 .
.
Пусть T 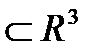 - открытое выпуклое множество,
- открытое выпуклое множество, 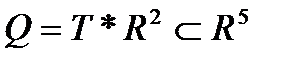 ,
, 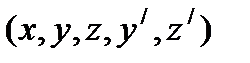 - текущая точка множества Q,
- текущая точка множества Q, 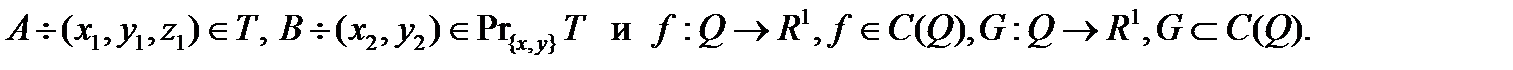
Вектор-функцию 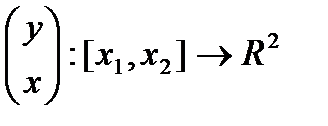
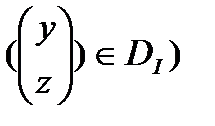 назовем допустимой, если
назовем допустимой, если 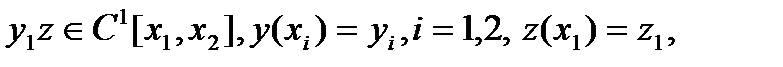
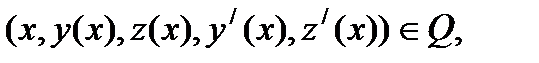
 ,
, 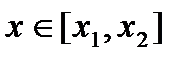 . (3)
. (3)
Каждой вектор-функции 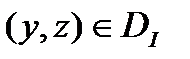 поставим в соответствие действительное число по формуле
поставим в соответствие действительное число по формуле
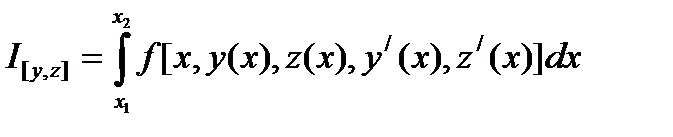 . Требуется минимизировать I на
. Требуется минимизировать I на 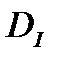 . Это задача Лагранжа с одной неголономной связью. Для
. Это задача Лагранжа с одной неголономной связью. Для 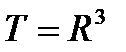 она имеет вид:
она имеет вид: 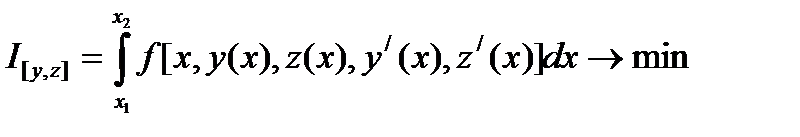 ,
, 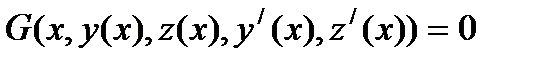
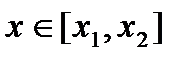 ,
, 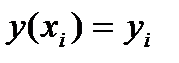 , I=1,2, z(x
, I=1,2, z(x 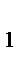 )=
)= 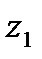 . Пусть вектор – функция
. Пусть вектор – функция 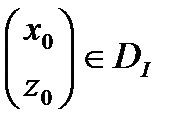 , являющаяся решением задачи Лагранжа с одной неголономной связью, дополнительно удовлетворяет условиям:
, являющаяся решением задачи Лагранжа с одной неголономной связью, дополнительно удовлетворяет условиям:
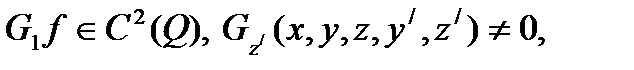 если
если 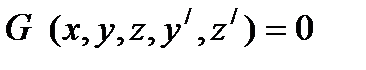 . Введём обозначения:
. Введём обозначения: 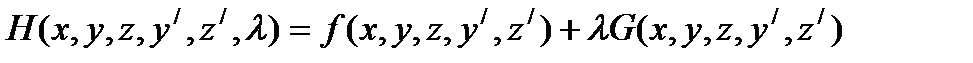 ,
, 
Теорема 2 Пусть 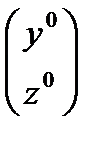 - решение задачи Лагранжа с одной неголономной связью. Тогда найдется функция
- решение задачи Лагранжа с одной неголономной связью. Тогда найдется функция 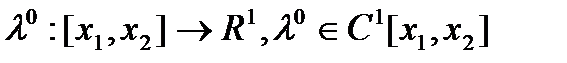 , что
, что 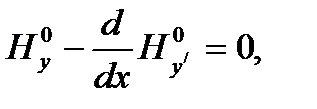
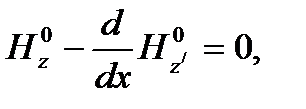
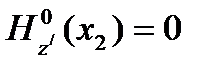
 2015-01-21
2015-01-21 643
643








