2015-01-21
403
Сформулируем достаточные условия существования решения задачи оптимального управления следующего вида:
, 
.
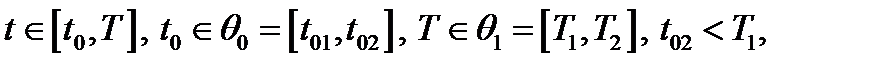
Относительно данных сделаем предположения:
1) 
- компактно;
2) мн-во 
компактно;
3) множество 
выпукло для всех 
;
4) существует константа 
, для которой справедливо неравенство 
.
Класс допустимых уравнений отождествляется с функциями, интегрируемыми по Лебегу на интервале управления.
Теорема 1. Пусть выполнены предположения 1) - 4) и множество 
. Тогда существует четверка 
, на которой функционал 
достигает минимума.
Замечание 1. В теории оптимального управления часто применяют следующие обозначения. Если 
некоторая функция, то 
ее значение в точке 
, а 
- сама функция, как элемент функционального пространства.
Замечание 2. Если функционал качества управления имеет вид 
, где 
. Первое слагаемое называется интегральным, а второе терминальным, а сам функционал – функционалом Больца. Если 
, то получаем функционал Майера, а в случае 
- функционал Лагранжа.
