В линейных задачах Теории оптимального уравнения дифференциальное уравнение принимает вид 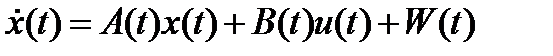 (*), где A(t) – где квадратная матрица
(*), где A(t) – где квадратная матрица 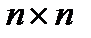 , B(t) – матрица
, B(t) – матрица 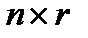 , W(t) – вектор
, W(t) – вектор 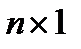 ,
, 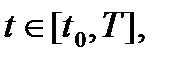 а функции
а функции 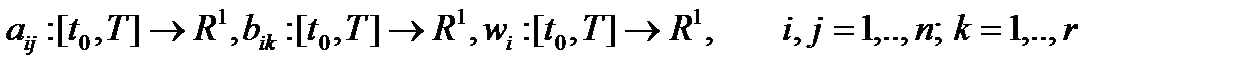 непрерывна по t. К уравнению (*) можно перейти непосредственно моделируя реальный динамический объект, а также в результате линеаризации дифференциальных уравнений его движения, когда исходная модель не линейна.
непрерывна по t. К уравнению (*) можно перейти непосредственно моделируя реальный динамический объект, а также в результате линеаризации дифференциальных уравнений его движения, когда исходная модель не линейна.
Линейную задачу теории оптимального уравнения называют задачей линейного быстродействия, если
1) уравнение (*) однородно, т.е. W(t)=0, 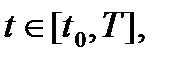 а A и B – постоянные;
а A и B – постоянные;
2) минимизируемый функционал имеет форму Лагранжа при 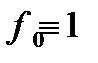 ;
;
3) начальный момент 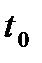 фиксирован;
фиксирован;
4) конечный момент 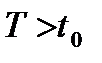 не фиксирован;
не фиксирован;
5) левый и правый концы траектории закреплены, т.е. 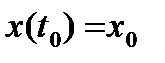 ,
, 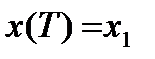 ;
;
6) фазовые ограничения отсутствуют, 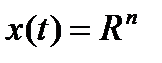 ;
;
7) область изменения управляющих параметров имеет вид:
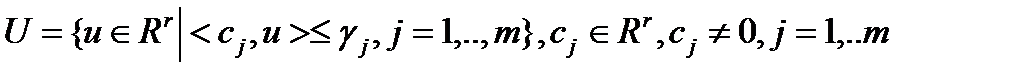 , ограничена, содержит в себе точку O, которая не является для нее угловой; U – выпуклый ограниченный многогранник.
, ограничена, содержит в себе точку O, которая не является для нее угловой; U – выпуклый ограниченный многогранник.
Опр.1 Подпространство 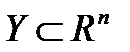 называется инвариантным относительно линейного преобразования
называется инвариантным относительно линейного преобразования 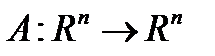 , если
, если 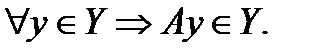 Оно называется собственным, если не совпадает со всем
Оно называется собственным, если не совпадает со всем 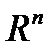 .
.
Замечание: 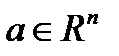 принадлежит инвариантному подпространству относительно линейного преобразования A в том и только том случае, если
принадлежит инвариантному подпространству относительно линейного преобразования A в том и только том случае, если 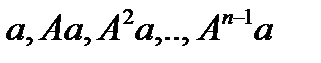 - линейно зависимы.
- линейно зависимы.
Опр.2 В задаче линейного быстродействия выполнено условие общности положения, если для любого вектора w, параллельно какому-либо ребру U, вектор Bw не принадлежит никакому собственному инвариантному подпространству относительно линейного преобразования A, т.е. 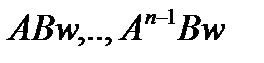 линейно независимы.
линейно независимы.
Для задачи линейного быстродействия дифференциальное уравнение движения имеет вид 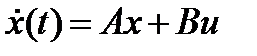 (1), минимизируемый функционал
(1), минимизируемый функционал 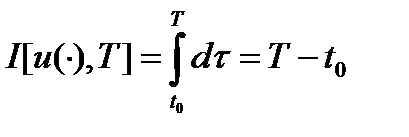 , функция Гамильтона-Понтрягина при
, функция Гамильтона-Понтрягина при 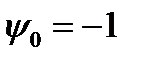 .
. 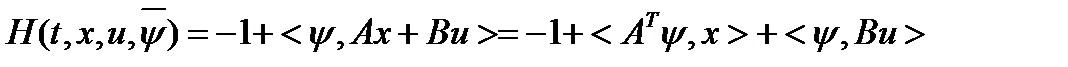 (2) и система сопряженных уравнений
(2) и система сопряженных уравнений 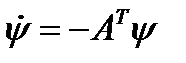 (3).
(3).
Лемма1. Пусть 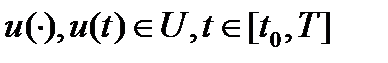 уравнение на
уравнение на 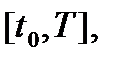
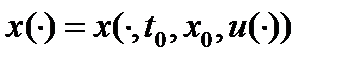 - порожденное им движение и
- порожденное им движение и 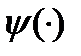 - решение сопряженного уравнения (3). Тогда
- решение сопряженного уравнения (3). Тогда 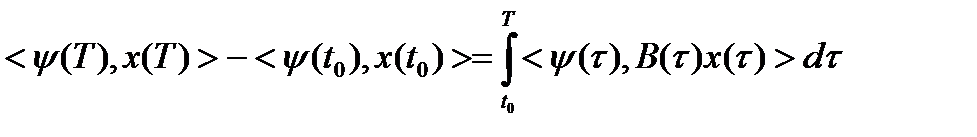 (4)
(4)
Лемма2. Пусть 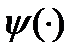 - нетривиальное решение уравнения (3). Для того, чтобы вектор
- нетривиальное решение уравнения (3). Для того, чтобы вектор 
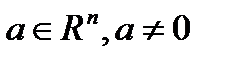 принадлежал собственному инвариантному относительно преобразования A подпространству, достаточно выполнения равенства
принадлежал собственному инвариантному относительно преобразования A подпространству, достаточно выполнения равенства 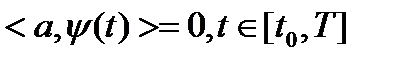 при некотором
при некотором 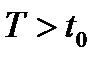 .
.
 2015-01-21
2015-01-21 1020
1020
