Рассмотрим автономную задачу оптимального управления с незакрепленным временем:
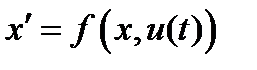 (1),
(1), 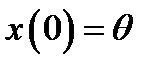 ,
, 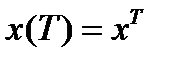 (2)
(2)
требуется минимизировать функционал 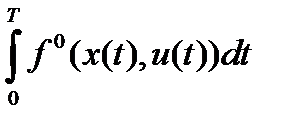 путем выбора вектора допустимого управления
путем выбора вектора допустимого управления  . Для эффективного и сжатого формулирования необходимых условий оптимальности вектора параметров управления, рассмотрим сопряженную систему линейных дифференциальных уравнений первого порядка для дополнительных переменных
. Для эффективного и сжатого формулирования необходимых условий оптимальности вектора параметров управления, рассмотрим сопряженную систему линейных дифференциальных уравнений первого порядка для дополнительных переменных 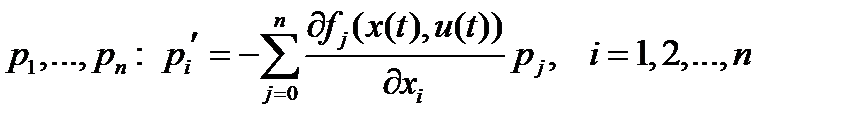 (3)
(3)
и функция Гамильтона-Понтрягина задачи оптимального управления 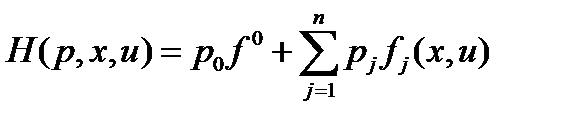 . Вектор
. Вектор  - вектор сопряженных переменных. Необходимое условие оптимальности, известное как принцип максимума Понтрягина формулируются так:
- вектор сопряженных переменных. Необходимое условие оптимальности, известное как принцип максимума Понтрягина формулируются так:
Теорема 1. Чтобы вектор параметров управления 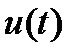 и соответствующая траектория
и соответствующая траектория 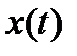 , описываемая формулами (1) и (2), были оптимальными, необходимо, чтобы существовало решение
, описываемая формулами (1) и (2), были оптимальными, необходимо, чтобы существовало решение 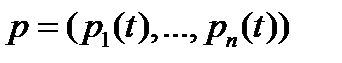 сопряженной системы (3) и константа
сопряженной системы (3) и константа 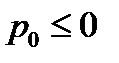 такие, что
такие, что 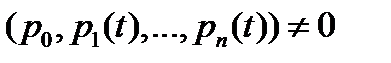 и
и 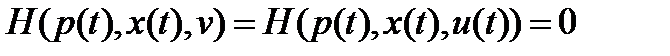 (4) для всех векторов
(4) для всех векторов  в каждой точке
в каждой точке 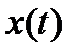 оптимальной траектории
оптимальной траектории 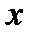 , где
, где 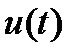 - вектор параметров управления.
- вектор параметров управления.
Замечание: Фраза «в каждой точке» подразумевает, что если 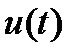 кусочно-непрерывная, то условие (4) справедливо в точках непрерывности
кусочно-непрерывная, то условие (4) справедливо в точках непрерывности 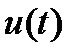 ; если
; если 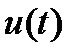 ограничена и измерима, то (4) справедливо почти всюду.
ограничена и измерима, то (4) справедливо почти всюду.
Рассмотрим пример 1 из Л. 14. Сопряженная система будет иметь вид:  . Решение её
. Решение её 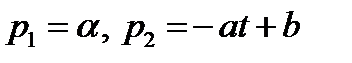 . Гамильтониан системы:
. Гамильтониан системы: 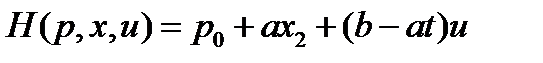 . Т.к.
. Т.к. 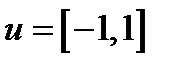 , то из принципа максимума Понтрягина следует
, то из принципа максимума Понтрягина следует 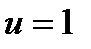 , если
, если 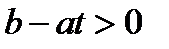 и
и  , если
, если 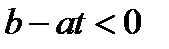 . Как видно из предыдущего примера, переменную
. Как видно из предыдущего примера, переменную 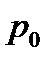 можно исключить из задач об оптимальном быстродействии. Заменим (4) условием: существует невырожденное решение
можно исключить из задач об оптимальном быстродействии. Заменим (4) условием: существует невырожденное решение 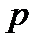 .
. 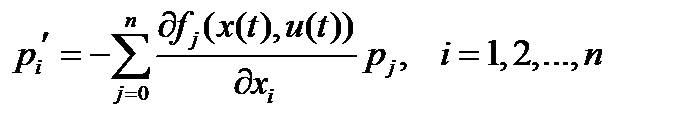 , что при
, что при 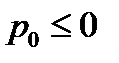 неравенство
неравенство 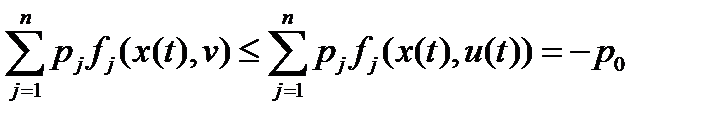 (5) имеет место
(5) имеет место 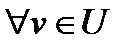 в каждой точке оптимальной траектории
в каждой точке оптимальной траектории 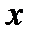 .
.
Для неавтономных задач с закрепленным временем непосредственно из принципа максимума следует, что должно существовать 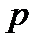 - решение системы (3), что для некоторой константы
- решение системы (3), что для некоторой константы 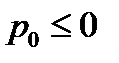 ,
, 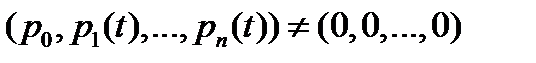 ,
, 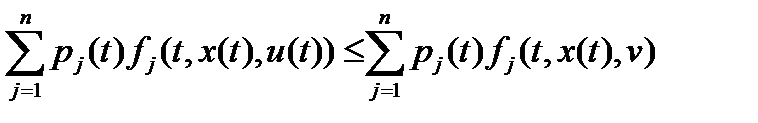 при
при 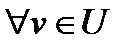 в каждой точке оптимальной траектории
в каждой точке оптимальной траектории 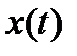 . (
. (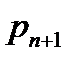 появляется благодаря введению новой переменной состояния
появляется благодаря введению новой переменной состояния 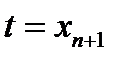 ).
).
Рассмотрим пример 2 из Л. 14. Получаем 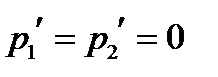 и значит
и значит 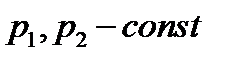 . Таким образом,
. Таким образом, 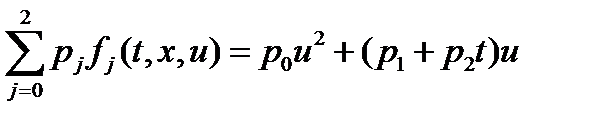 , где
, где 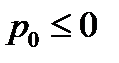 . Данная функция достигает максимума при
. Данная функция достигает максимума при 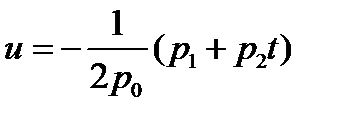 . При
. При 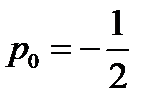 ,
, 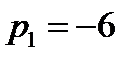 ,
, 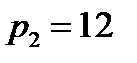 получаем следующую траекторию
получаем следующую траекторию 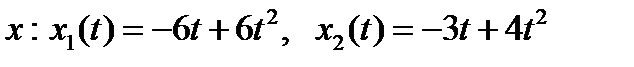 . Функционал
. Функционал 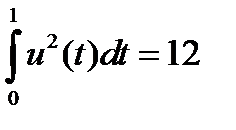 .
.
 2015-01-21
2015-01-21 1263
1263








