Сформулируем принцип оптимальности для динамических задач, представляющихся классическими задачами вариационного исчисления с ограничениями типа равенств и неравенств.
Пусть требуется найти 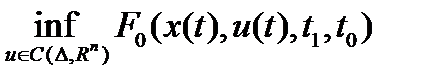 (0) при ограничениях вида:
(0) при ограничениях вида:
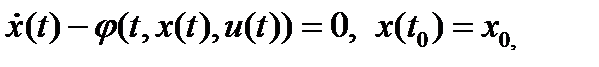 (1),
(1), 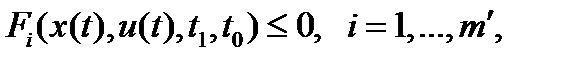 (2)
(2)
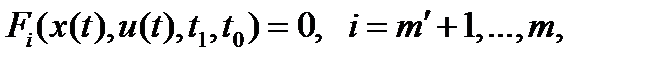 (3) в пространстве
(3) в пространстве 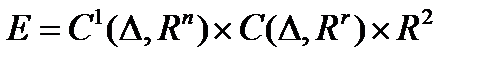 , где
, где 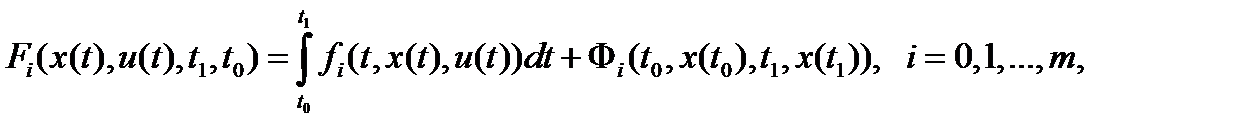
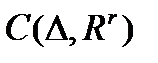 - пространство непрерывных функций;
- пространство непрерывных функций; 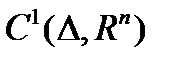 - пространство дифференцируемых функций,
- пространство дифференцируемых функций,  - заданный конечный отрезок,
- заданный конечный отрезок, 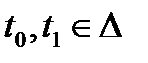 ;
; 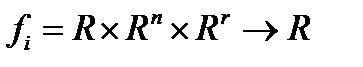 - функция
- функция 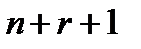 переменных;
переменных;
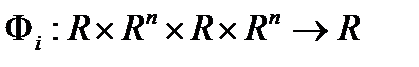 - функция
- функция 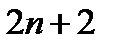 переменных;
переменных; 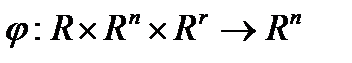 - функция
- функция 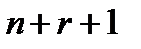 переменных;
переменных; 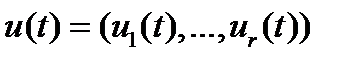 - вектор-функция управления;
- вектор-функция управления; 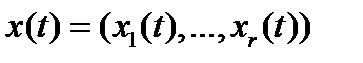 - вектор-функция фазовой переменной;
- вектор-функция фазовой переменной; 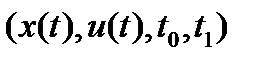 - управляющий процесс в задаче Лагранжа, если
- управляющий процесс в задаче Лагранжа, если 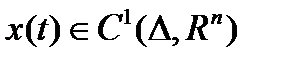 ,
, 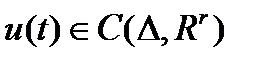 ,
, 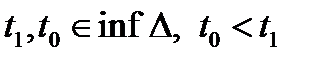 и всюду на
и всюду на 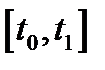 выполнится дифференциальная связь, задаваемая (1); если же при этом выполняются ограничения
выполнится дифференциальная связь, задаваемая (1); если же при этом выполняются ограничения 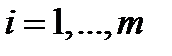 (2), (3), то четверка
(2), (3), то четверка 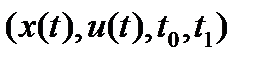 - допустимый управляющий процесс.
- допустимый управляющий процесс.
Теорема Эйлера- Лагранжа Пусть 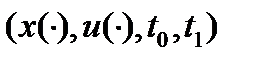 - оптимальный (в слабом смысле) процесс и при этом функции
- оптимальный (в слабом смысле) процесс и при этом функции 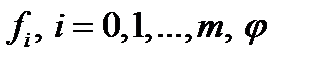 и их частные производные по
и их частные производные по 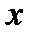 и
и 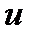 непрерывны в некоторой окрестности множества
непрерывны в некоторой окрестности множества 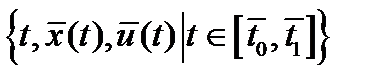 , а
, а 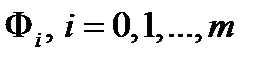 , непрерывно дифференцируемы в окрестности точки
, непрерывно дифференцируемы в окрестности точки 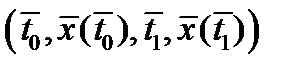 . Тогда найдутся множители Лагранжа и
. Тогда найдутся множители Лагранжа и 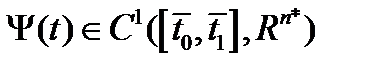 не равные одновременно нулю и такие, что для функции Лагранжа
не равные одновременно нулю и такие, что для функции Лагранжа 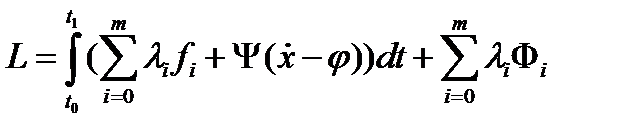 выполнены условия: а) стационарности по
выполнены условия: а) стационарности по 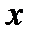 ,
, 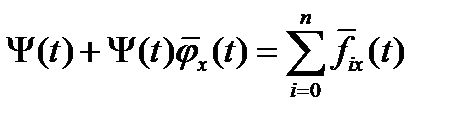 ; б) трансверсальности по
; б) трансверсальности по 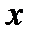 ,
, 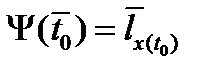 ,
, 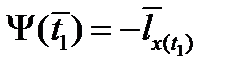 ,
, 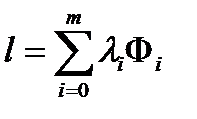 ;
;
в) стационарности по 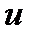 ,
, 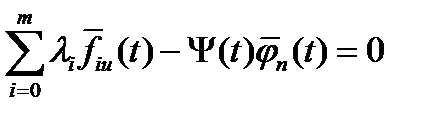 ; г) стационарности по
; г) стационарности по 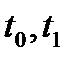 (для незакрепленных
(для незакрепленных 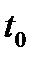 и
и 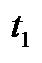 ),
), 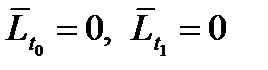 ; д) не отрицательности (только при наличии ограничений неравенств)
; д) не отрицательности (только при наличии ограничений неравенств) 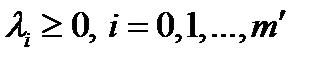 ; е) дополняющей нежесткости (только при наличии ограничений неравенств)
; е) дополняющей нежесткости (только при наличии ограничений неравенств)
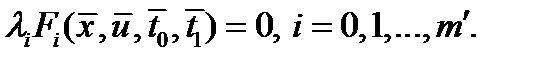
Замечание. 1)допустимый управляемый процесс 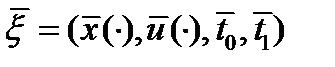 называется оптимальным (в слабом смысле) процессом, или слабым минимумом в задаче (0), если существует такое
называется оптимальным (в слабом смысле) процессом, или слабым минимумом в задаче (0), если существует такое 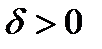 , что для любого допустимого управляемого процесса
, что для любого допустимого управляемого процесса 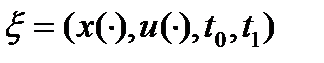 , удовлетворяющего условию
, удовлетворяющего условию 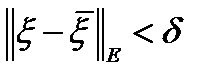 , выполнено неравенство
, выполнено неравенство 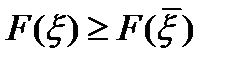 .
.
2) 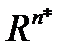 - арифметическое n-мерное пространство, сопряженное к
- арифметическое n-мерное пространство, сопряженное к 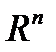 ,
, 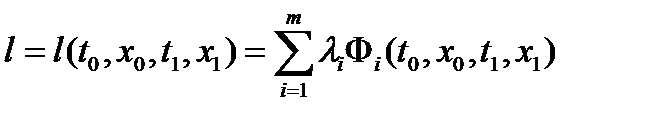 - терминант.
- терминант.
30. Необходимые условия в задаче теории оптимального управления
В случае выбора решений в динамических задачах оптимального управления в пространстве 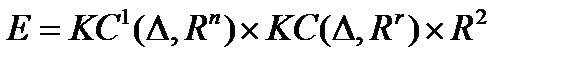 , когда
, когда 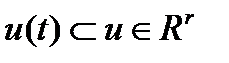 , т.е. в задачах вида
, т.е. в задачах вида
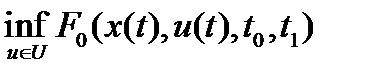 ,
, 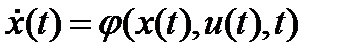 ,
, 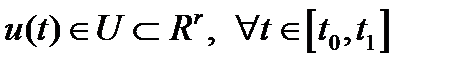 ,
, 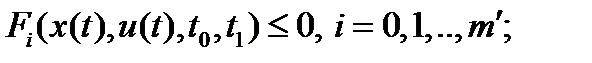
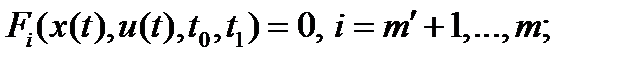
где 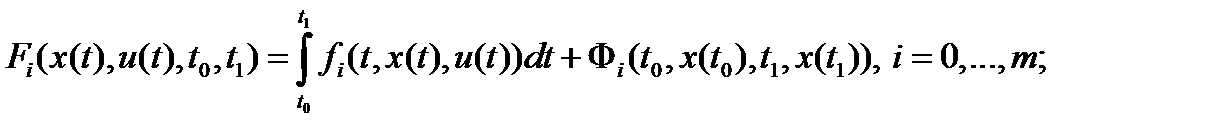
(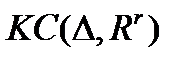 - пространство кусочно-непрерывных функций;
- пространство кусочно-непрерывных функций; 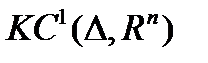 - пространство кусочно-дифференцируемых функций;
- пространство кусочно-дифференцируемых функций; 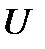 - произвольное множество из
- произвольное множество из 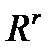 ;
; 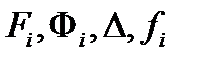 - раскрываются такие, как в задаче Лагранжа п.15.2), принцип оптимальности формируется как принцип максимума Понтрягина.
- раскрываются такие, как в задаче Лагранжа п.15.2), принцип оптимальности формируется как принцип максимума Понтрягина.
Теорема 1 (Необходимое условие экстремума) Пусть 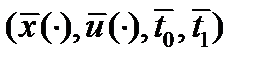 - оптимальный процесс в задаче оптимального управления, функции
- оптимальный процесс в задаче оптимального управления, функции 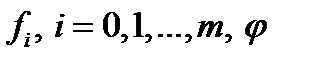 и их частные производные по
и их частные производные по 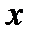 непрерывности во множестве
непрерывности во множестве 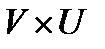 , где
, где 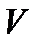 - некоторая окрестность множества
- некоторая окрестность множества 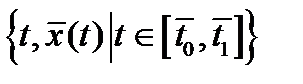 , а
, а 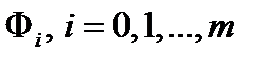 непрерывно дифференцируемы в окрестности точки
непрерывно дифференцируемы в окрестности точки 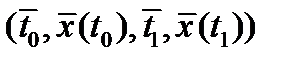 . Тогда найдутся множители Лагранжа
. Тогда найдутся множители Лагранжа 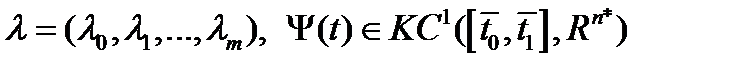 , не равные одновременно нулю и такие, что для функции Лагранжа
, не равные одновременно нулю и такие, что для функции Лагранжа 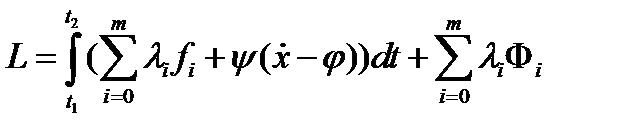 выполнены условия:
выполнены условия:
а) стационарности по 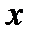 - уравнения Эйлера,
- уравнения Эйлера,
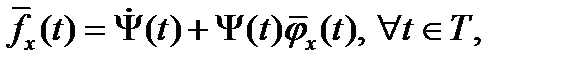
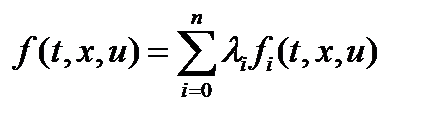 , б) трансверсальности по
, б) трансверсальности по 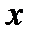 ,
, 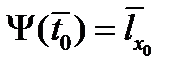 ,
, 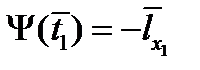 ,для терминантов на
,для терминантов на 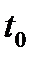 и
и 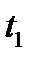 ; в) оптимальности по
; в) оптимальности по 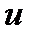
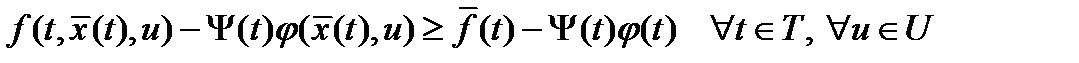 ; г) стационарности по
; г) стационарности по 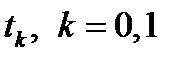 (только для незакрепленных
(только для незакрепленных 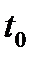 ,
, 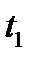 )
) 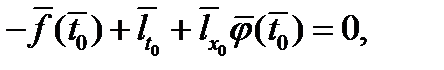
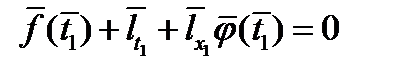 ; д) дополняющей нежесткости (при наличии ограничений неравенств)
; д) дополняющей нежесткости (при наличии ограничений неравенств) 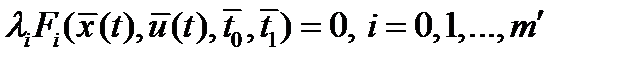 ; е) неотрицательности (при наличии ограничений неравенств)
; е) неотрицательности (при наличии ограничений неравенств) 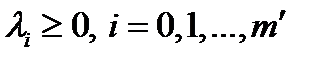 .
.
Здесь 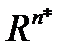 - арифметическое n-мерное пространство, сопряженное к
- арифметическое n-мерное пространство, сопряженное к 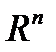 ,
, 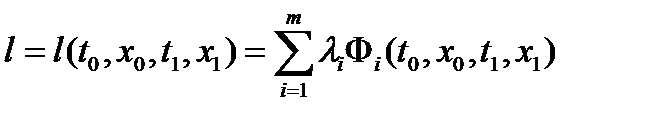 - терминант.
- терминант.
31. Принцип максимума Понтрягина для простейшей задачи оптимального управления
Задачу теории оптимального управления назовем простейшей, если для нее начальный и конечный моменты времени фиксированы, левый конец закреплен, правый – свободен, фазовые ограничения отсутствуют, а ограничение на вектора управляющих параметров стационарны, т. е. Из (1)-(4) (п. 14.1) получаем следующую краткую запись для простейшей задачи оптимального управления:
дано: 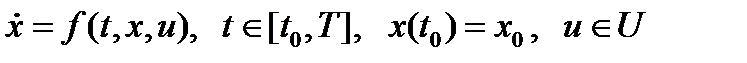 ,
, 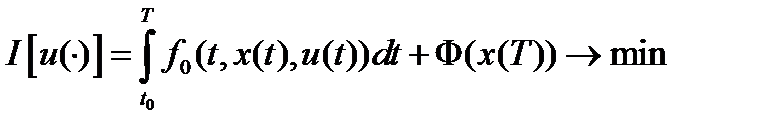 (1)
(1)
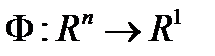 - непрерывно дифференцируема по совокупности своих параметров. Пусть
- непрерывно дифференцируема по совокупности своих параметров. Пусть 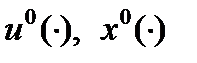 - оптимальное управление и оптимальная траектория в задаче (1). Если
- оптимальное управление и оптимальная траектория в задаче (1). Если 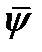 - вектор сопряженных переменных, то т. к. Сопряженная система дифференцируемых уравнений, отвечающая паре
- вектор сопряженных переменных, то т. к. Сопряженная система дифференцируемых уравнений, отвечающая паре 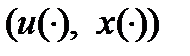 имеет вид
имеет вид 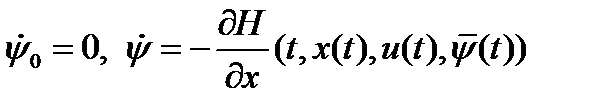 , то если
, то если 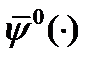 решение сопряженной системы дифференциальных уравнений, отвечающей этой паре при граничных условиях
решение сопряженной системы дифференциальных уравнений, отвечающей этой паре при граничных условиях 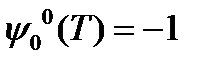 и
и 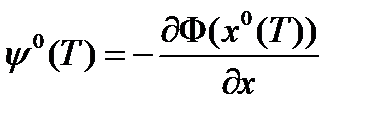 , (2) то
, (2) то 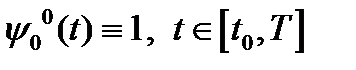 .
.
Теорема 1. (Принцип максимума Понтрягина ) В любой момент времени 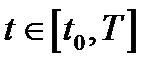 имеет место равенство
имеет место равенство 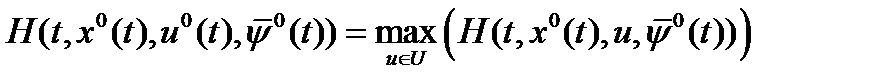 . (
. (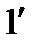 )
)
Практическое применение задачи Т.1 осуществляется следующим образом для поиска решения задачи управления. Выражение для 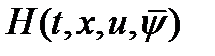 , в котором полагают
, в котором полагают 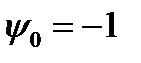 , рассматривается как функция
, рассматривается как функция 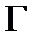 переменных
переменных 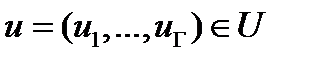 , а остальные переменные при этом считаются параметрами. Для каждого фиксированного набора
, а остальные переменные при этом считаются параметрами. Для каждого фиксированного набора 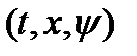 решается задача математического программирования
решается задача математического программирования 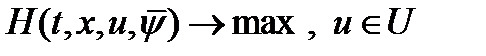 . Решением ее будет
. Решением ее будет 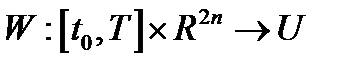 . Таким образом
. Таким образом 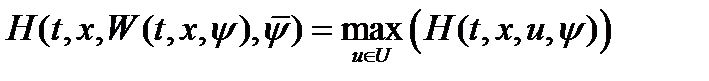 . В ряде случаев функцию
. В ряде случаев функцию 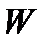 можно выписать в явном виде. Если
можно выписать в явном виде. Если 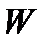 построена, то можно рассмотреть следующую систему из
построена, то можно рассмотреть следующую систему из 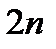 дифференциальных уравнений относительно
дифференциальных уравнений относительно 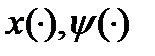 :
: 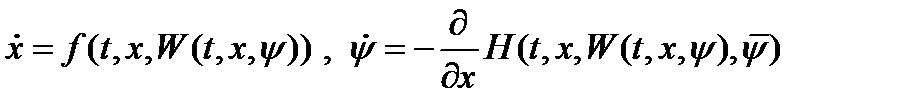 , (3), где
, (3), где 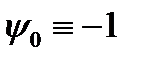 . Для определения
. Для определения 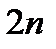 произвольных постоянных имеется
произвольных постоянных имеется 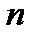 граничных условий на левом конце:
граничных условий на левом конце: 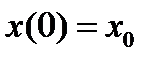 -, и на правом:
-, и на правом: 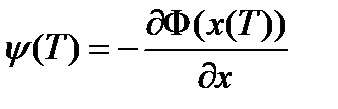 . (4)
. (4)
Опр.1 Пара 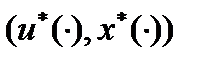 удовлетворяет условиям принципа максимума, если
удовлетворяет условиям принципа максимума, если 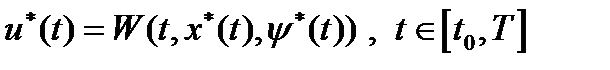 , а
, а 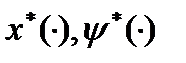 - решение системы (3) при граничных условиях (4) и
- решение системы (3) при граничных условиях (4) и 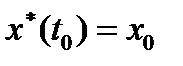 .
.
Пары, удовлетворяющие условиям принципа максимума назовем стационарными.
Рассмотрим пример применения принципа максимума Понтрягина при решении простейшей задачи теории оптимального управления:
Пример1 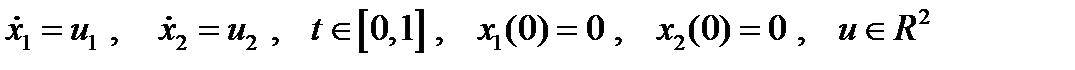
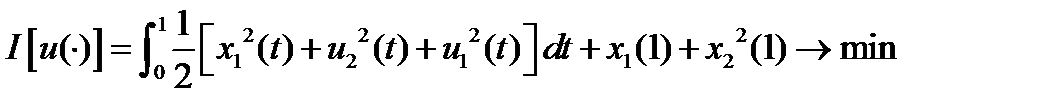
Функция Гамильтона-Понтрягина (с учетом 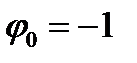 ) имеет вид:
) имеет вид: 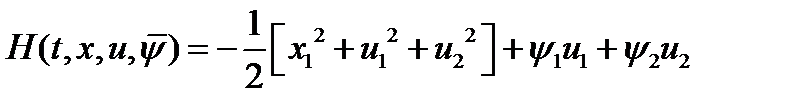 . Вектор-функция
. Вектор-функция 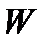 из условия
из условия 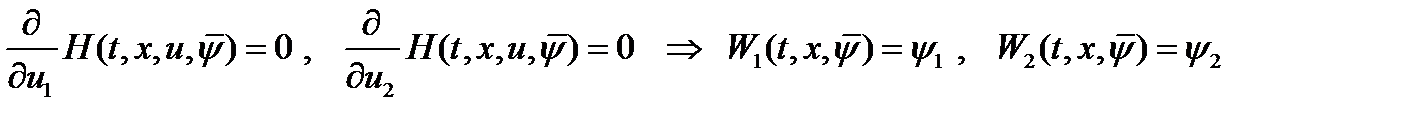 .
.
Основная и сопряженная система дифференциальных уравнений:
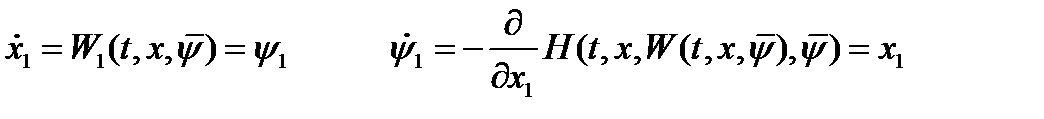
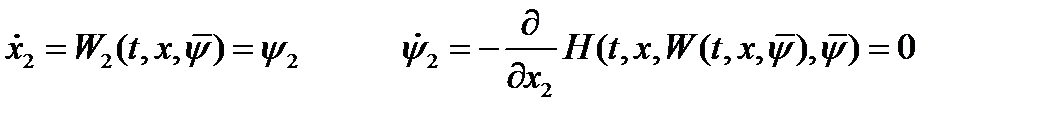 .
.
Интегрируя их совместно, получаем:
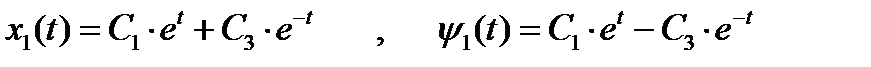
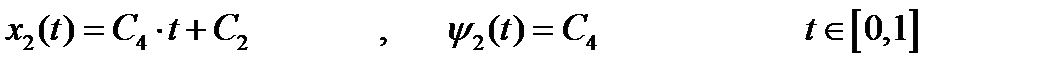 (5)
(5)
Из граничных условий: 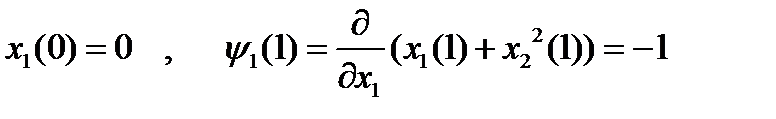
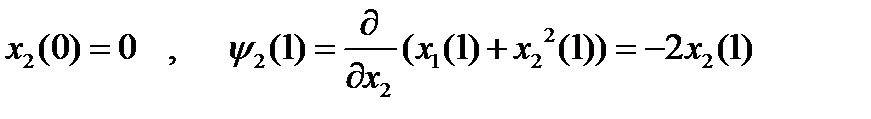 , которые в силу (5) принимают вид:
, которые в силу (5) принимают вид: 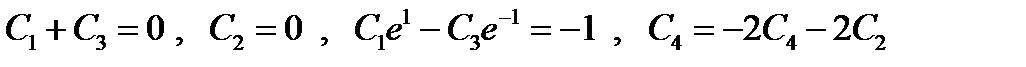 , откуда
, откуда 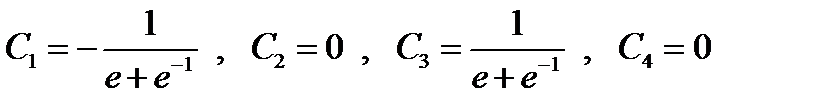 ,
, 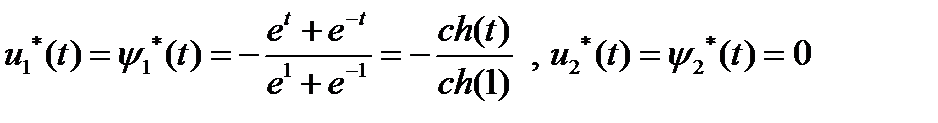
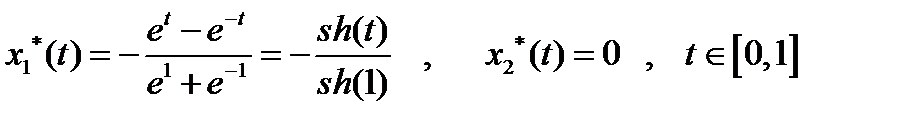
Для доказательства теоремы 1 дополнительно положим, что 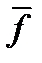 и
и 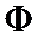 непрерывно дифференцируемы по
непрерывно дифференцируемы по 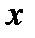 и
и 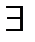 константа
константа 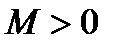 , для которой
, для которой 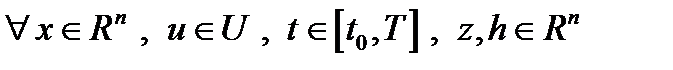 справедливы неравенства:
справедливы неравенства: 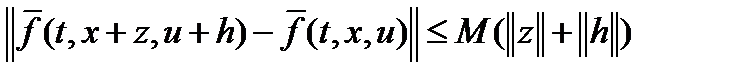 ,
,
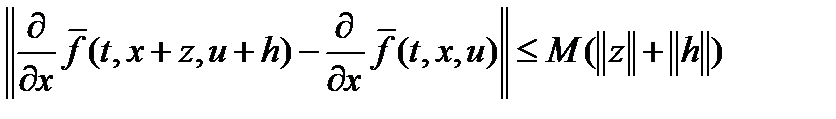 , (6)
, (6)
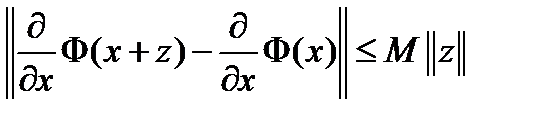 .
.
Пусть 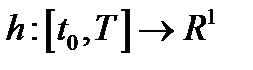 - кусочно-непрерывная функция, для которой:
- кусочно-непрерывная функция, для которой: 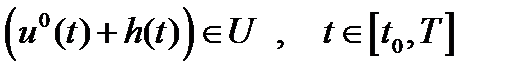 . Полагаем
. Полагаем 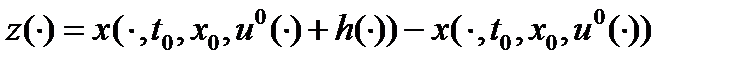 .
.
Сформулируем ряд утверждений, которые используются в доказательстве Т.1.
Лемма 1. Имеет место равенство: 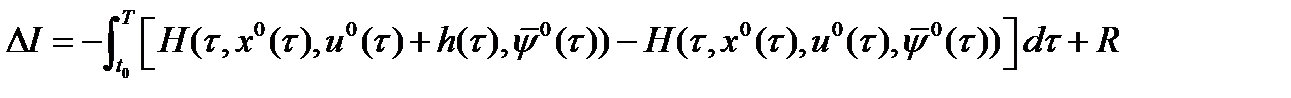 , (7), где
, (7), где 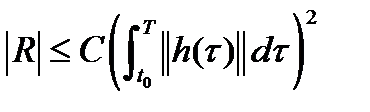 (8),
(8), 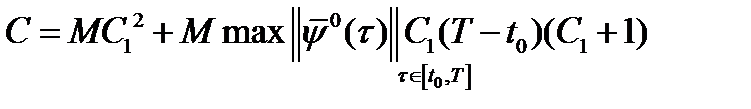 .
.
Лемма 2. Имеет место равенство:
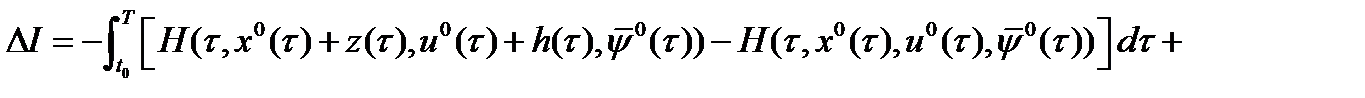
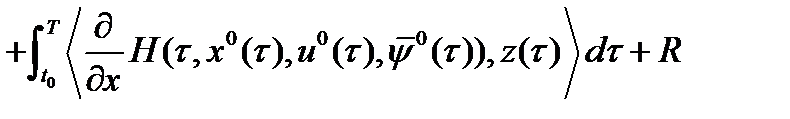 , (9), где
, (9), где 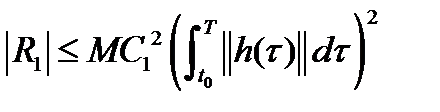 .
.
Лемма 3. Справедлива оценка: 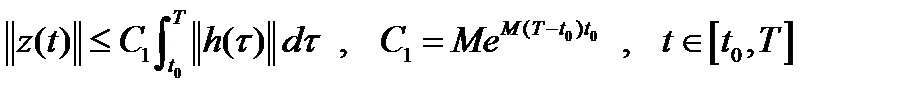 .
.
Пусть 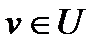 ,
, 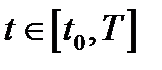 , и
, и 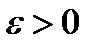 столь мало, что
столь мало, что 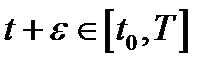 .
.
Функцию 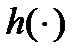 определим формулой:
определим формулой:
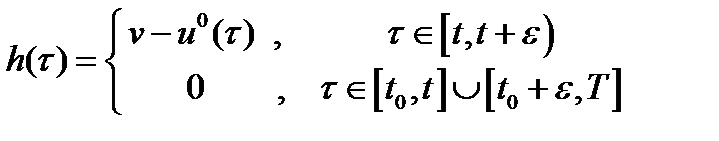 (10)
(10)
Очевидно, что 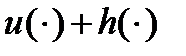 кусочно-непрерывная функция и для всех
кусочно-непрерывная функция и для всех 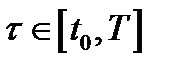 выполнено включение
выполнено включение 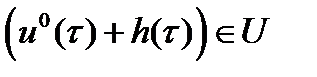 . Таким образом, для управления
. Таким образом, для управления 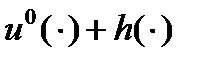 и движения
и движения 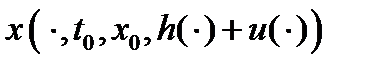 в соответствии с леммой 1 справедлива оценка (7), (8), которая в силу (10) имеет вид:
в соответствии с леммой 1 справедлива оценка (7), (8), которая в силу (10) имеет вид: 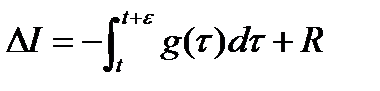 (11), где
(11), где 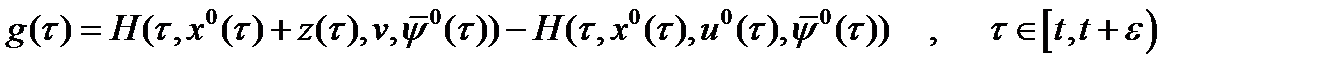
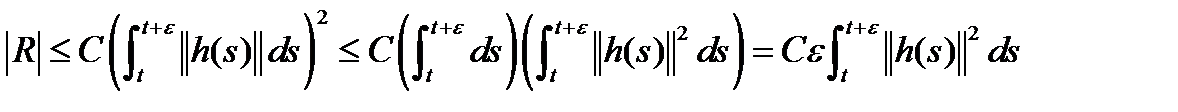 (12)
(12)
При достаточно малых 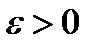 функция
функция 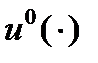 непрерывна на
непрерывна на 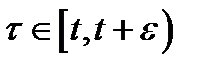 , поэтому
, поэтому
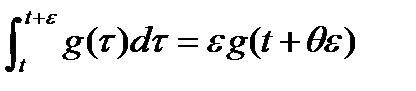 ,
, 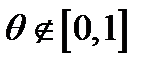 (13)
(13)
Из оптимальности пары 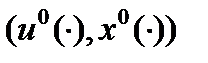 следует неравенство
следует неравенство 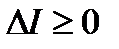 . Тогда в силу (11) - (13) заключаем:
. Тогда в силу (11) - (13) заключаем: 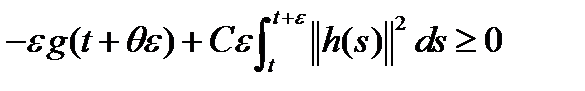 (14)
(14)
Поделив обе части неравенства (14) на положительное 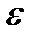 и устремив
и устремив 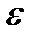 к нулю получаем
к нулю получаем 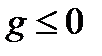 . Из определения
. Из определения 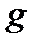 выводим:
выводим: 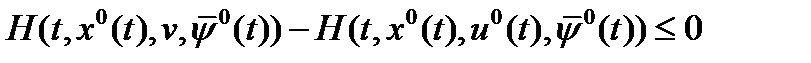 (15)
(15)
В силу произвольности 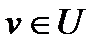 из неравенства (15) следует справедливость условия (2) для всех
из неравенства (15) следует справедливость условия (2) для всех 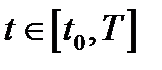 . Чтобы доказать его для
. Чтобы доказать его для 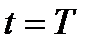 надо взять
надо взять 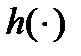 в виде:
в виде:
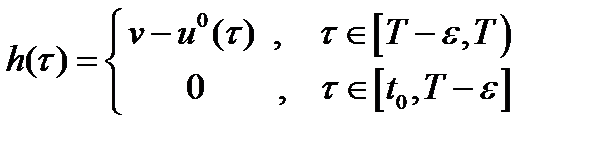
и провести аналогичные рассуждения. Теорема 1 доказана.
Рассмотрим случай простейшей задачи с нефиксированной продолжительностью процесса: 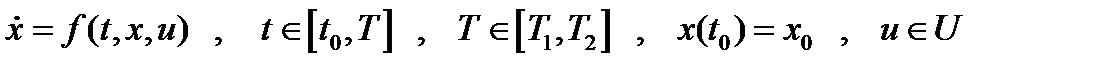 ,
,
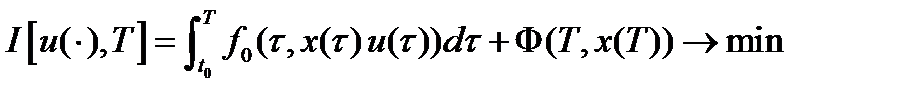
Если рассмотреть вспомогательную задачу с фиксированной продолжительностью процесса, то если 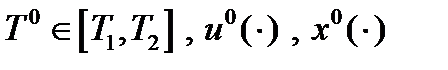 - решение основной задачи, то
- решение основной задачи, то 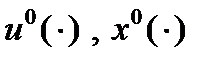 будет решением вспомогательной задачи при условии
будет решением вспомогательной задачи при условии 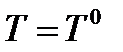 . Но по Т.1 для пары
. Но по Т.1 для пары 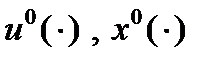 будет выполняться условие принципа максимума Понтрягина при
будет выполняться условие принципа максимума Понтрягина при 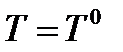 . Однако условий принципа максимума недостаточно для выделения изолированных пар
. Однако условий принципа максимума недостаточно для выделения изолированных пар 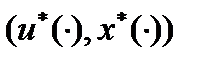 , среди которых только и могло бы находиться решение исходной задачи с нефиксированной длительностью процесса. Это объясняется тем, что помимо (2) и произвольных констант интегрирования в общем решении системы дифференциальных уравнений (3) определению подлежит еще и момент
, среди которых только и могло бы находиться решение исходной задачи с нефиксированной длительностью процесса. Это объясняется тем, что помимо (2) и произвольных констант интегрирования в общем решении системы дифференциальных уравнений (3) определению подлежит еще и момент 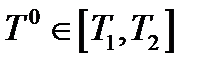 . Дополнительные условия, которым удовлетворяет
. Дополнительные условия, которым удовлетворяет 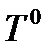 определяются следующей теоремой.
определяются следующей теоремой.
Теорема 2. Пусть 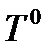 - оптимальный конечный момент времени в простейшей задаче оптимального управления с нефиксированной длительностью процесса. Тогда
- оптимальный конечный момент времени в простейшей задаче оптимального управления с нефиксированной длительностью процесса. Тогда
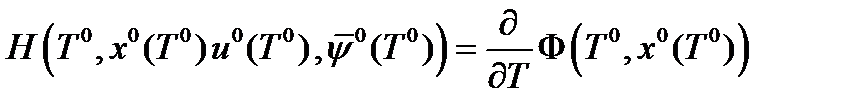 .
.
 2015-01-21
2015-01-21 1866
1866
