2015-01-21
698
Как известно, проекцией точки A на прямую (плоскость) служит основание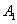 
перпендикуляра 
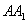, опущенного из этой точки на прямую (плоскость).
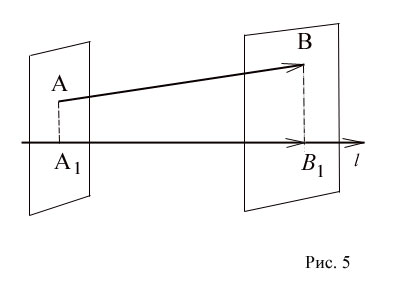Пусть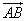 
- произвольный вектор (Рис. 5), а 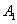и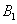 
- проекции его начала (точки A) и конца (точки B) на ось l. (Для построения проекции точки A) на прямую проводим через точку A плоскость, перпендикулярную прямой. Пересечение прямой и плоскости определит искомую проекцию.
Составляющей вектора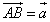 
на оси l называется такой вектор 
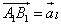, лежащий на этой оси, начало которого совпадает с проекцией начала, а конец - с проекцией конца вектора .
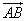Проекцией вектора 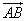на ось l называется число
,
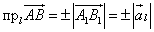равное длине составляющего вектора на этой оси, взятое со знаком плюс, если направление составляюшей совпадает с направлением оси l, и со знаком минус, если эти направления противоположны.
Основные свойства проекций вектора на ось:
1. Проекции равных векторов на одну и ту же ось равны между собой.
2. При умножении вектора на число его проекция умножается на это же число.
3. Проекция суммы векторов на какую-либо ось равна сумме проекций на эту же ось слагаемых векторов.
4. Проекция вектора на ось равна произведению длины проектируемого вектора на косинус угла между вектором и осью:
