Дифференциал функции в точке 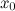 равен приращению ординаты касательной, проведенной к графику функции в этой точке, соответствующему приращению аргумента
равен приращению ординаты касательной, проведенной к графику функции в этой точке, соответствующему приращению аргумента  .
.
Пусть функция y = f (x) дифференцируема при некотором значении переменной x. Следовательно, в точке x существует конечная производная
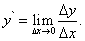
Тогда по определению предела функции разность
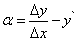 (1)
(1)
является бесконечно малой величиной при 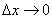 . Выразив из равенства (1) приращение функции, получим
. Выразив из равенства (1) приращение функции, получим
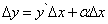 (2)
(2)
(величина 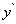 не зависит от
не зависит от 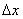 , т. е. остаётся постоянной при
, т. е. остаётся постоянной при 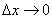 ).
).
Если 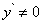 , то в правой части равенства (2) первое слагаемое
, то в правой части равенства (2) первое слагаемое 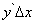 линейно относительно
линейно относительно 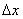 . Поэтому при
. Поэтому при
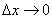
оно является бесконечно малой того же порядка малости, что и 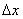 . Второе слагаемое
. Второе слагаемое 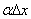 - бесконечно малая более высокого порядка малости, чем первое, так как их отношение
- бесконечно малая более высокого порядка малости, чем первое, так как их отношение  стремится к нулю при
стремится к нулю при
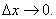
Поэтому говорят, что первое слагаемое формулы (2) является главной, линейной относительно 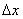 частью приращения функции; чем меньше
частью приращения функции; чем меньше 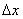 , тем большую долю приращения составляет эта часть. Поэтому при малых значениях
, тем большую долю приращения составляет эта часть. Поэтому при малых значениях 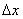 (и при
(и при 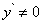 ) приращение функции можно приближенно заменить его главной частью
) приращение функции можно приближенно заменить его главной частью 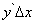 , т.е.
, т.е.
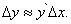 (3)
(3)
Эту главную часть приращения функции называют дифференциалом данной функции в точке x и обозначают
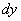
или
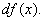
Следовательно,
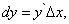 (4)
(4)
или
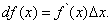 (5)
(5)
Итак, дифференциал функции y = f (x) равен произведению её производной на приращение независимой переменной.
Дифференциал обладает свойствами, аналогичными свойствам производной:
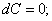 (С – постоянная величина) (8)
(С – постоянная величина) (8)
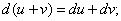 (9)
(9)
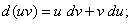 (10)
(10)
 (11)
(11)
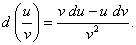 (12)
(12)
Формулы (8) – (12) получаются из соответствующих формул для производной умножением обеих частей каждого равенства на 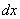 .
.
Рассмотрим дифференциал сложной функции. Пусть 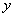 - сложная функция
- сложная функция 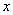 :
:
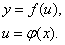
Дифференциал
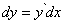
этой функции, используя формулу для производной сложной функции, можно записать в виде
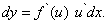
Но 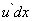 есть дифференциал функции
есть дифференциал функции 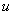 , поэтому
, поэтому
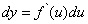 ,
,
т.е.
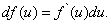 (13)
(13)
 2015-01-21
2015-01-21 390
390








