Следствие 1 (признак монотонности функции). Если в любой точке некоторого интервала производная функции неотрицательна (положительна), то функция не убывает (возрастает) на этом интервале.
Действительно, если — две точки нашего интервала и то по формуле (2)
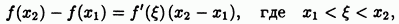
и, таким образом, знак разности, стоящей в левой части равенства, совпадает со знаком
Разумеется, аналогичное утверждение можно высказать о невозрастании (убывании) функции с неположительной (отрицательной) производной.
Замечание. На основании теоремы об обратной функции и следствия 1, в частности, можно заключить, что если на каком-то промежутке I числовая функция имеет положительную или отрицательную производную, то функция непрерывна на монотонна на имеет обратную функцию определенную на промежутке и дифференцируемую на нем.
Следствие 2 (критерий постоянства функции). Непрерывная на отрезке функция постоянна на нем тогда и только тогда, когда ее производная равна нулю в любой точке отрезка (или хотя бы интервала
Интерес представляет только доказательство того факта, что если на то для любых имеет место равенство Но это вытекает из теоремы Лагранжа, по которой
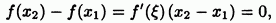
ибо лежит между
Замечание. Отсюда, очевидно, можно сделать следующий (как мы увидим, очень важный для интегрального исчисления) вывод: если производные двух функций совпадают на некотором промежутке, т. е. то на этом промежутке разность есть постоянная функция.
Полезным обобщением теоремы Лагранжа, которое тоже основано на теореме Ролля, является следующее
Утверждение 2 (теорема Коши о конечном приращении). Пусть — функции, непрерывные на отрезке и дифференцируемые в интервале
Тогда найдется точка такая, что
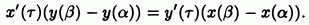
 2015-01-21
2015-01-21 2177
2177








