Теорема Лагранжа о конечном приращении

Следующее утверждение является одним из наиболее часто используемых и важных средств исследования числовых функций.

Теорема 1 (теорема Лагранжа о конечном приращении). Если функция непрерывна на отрезке и дифференцируема в интервале то найдется точка такая, что

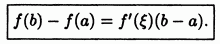
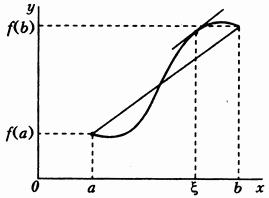
Рис. 21

Для доказательства рассмотрим вспомогательную функцию

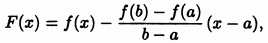
которая, очевидно, непрерывна на отрезке дифференцируема в интервале и на его концах принимает равные значения: Применяя к теорему Ролля, найдем точку в которой

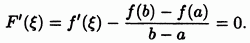
Замечания к теореме Лагранжа. 1° Геометрически теорема Лагранжа означает (рис. 21), что в некоторой точке где

касательная к графику функции будет параллельна хорде, соединяющей точки ибо угловой коэффициент последней равен

2° Если х интерпретировать как время, а — как величину перемещения за время частицы, движущейся вдоль прямой, то теорема Лагранжа означает, что скорость частицы в некоторый момент такова, что если бы в течение всего промежутка времени частица двигалась с постоянной скоростью то она сместилась бы на ту же величину Величину естественно считать средней скоростью движения в промежутке

3° Отметим, однако, что при движении не по прямой средней скорости в смысле замечания 2° может не быть. Действительно, пусть, например, частица движется по окружности единичного радиуса с постоянной угловой скоростью Закон ее движения, как мы знаем, можно записать в виде

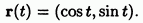
Тогда

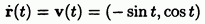
В моменты частица находится в одной и той же точке плоскости и равенство

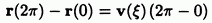
означало бы, что но это невозможно.

Однако мы сознаем, что зависимость между перемещением за некоторый промежуток времени и скоростью движения все же имеется. Она состоит в том, что даже вся длина пройденного пути не может превышать максимальной по величине скорости, умноженной на время в пути. Сказанное можно записать в следующей более точной форме:

Как будет в свое время показано, это естественное неравенство действительно всегда справедливо. Его тоже называют теоремой Лагранжа о конечном приращении, а формулу (2), справедливую только для числовых функций, часто называют теоремой Лагранжа о среднем значении (роль среднего в данном случае играет как величина скорости, так и точка лежащая между а и

4° Теорема Лагранжа важна тем, что она связывает приращение функции на конечном отрезке с производной функции на этом отрезке. До сих пор мы не имели такой теоремы о конечном приращении и характеризовали только локальное (бесконечно малое) приращение функции через производную или дифференциал в фиксированной точке.