Центральная предельная теорема (ЦПТ) для одинаково распределенных независимых случайных величин

Теорема. Пусть X₁,...,X_n,... последовательность независимых одинаково распределенных случайных величин с математическим ожиданием M[X_i] = m < ¥ и дисперсией D[X_i] = s² < ¥. Пусть 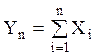, тогда при n ® ¥

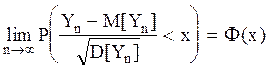(1)

где .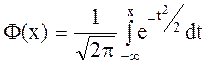

Доказательство: Обозначим

,

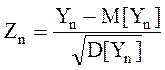тогда 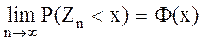и утверждение теоремы означает, что 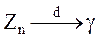~N(0,1) стандартная или стандартизированная нормальная случайная величина. Найдем математическое ожидание, дисперсию и подставим в Z _n

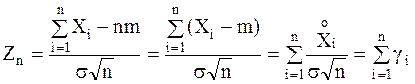
Пусть 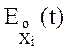- характеристическая функция центрированной случайной величины. Тогда

(*)

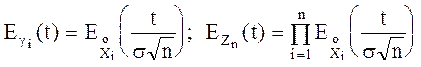Разложим характеристическую функцию 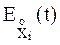в ряд Маклорена в окрестности точки t = 0

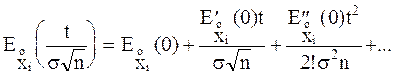
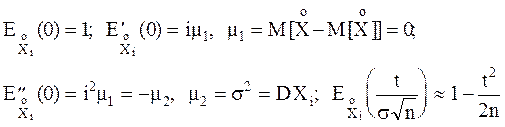
Подставим последнее выражение в (*), и получим

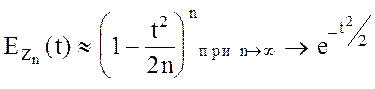
а это выражение есть характеристическая функция случайной величины g, распределенной по нормальному закону с M[g]=0; D[g]=1. По теореме единственности существует однозначное соответствие между характеристической функцией и функцией распределения, таким образом, 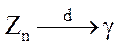и теорема доказана. š