Переменной называют величину 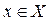 , принимающую значения из некоторого множества значений Х.
, принимающую значения из некоторого множества значений Х.
Если каждому значению переменной х из множества Х поставлено в соответствие по определенному правилу f единственное значение переменной у из множества Y, то говорят, что задана функция 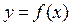 , определенная на множестве Х с множеством значений Y. При этом используют следующие названия:
, определенная на множестве Х с множеством значений Y. При этом используют следующие названия:
х ––– аргумент (независимая переменная);
у – значение функции (зависимая переменная);
Х – область определения функции (ООФ);
Y – множество значений функции (ОЗФ).
Функция 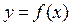 , область определения Х которой симметрична относительно начала координат, называется четной, если
, область определения Х которой симметрична относительно начала координат, называется четной, если 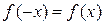 , и называется нечетной, если
, и называется нечетной, если 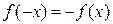 , "
, " 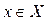 .
.
Примеры. y = cos x – четная функция, y = x 3 – нечетная функция, 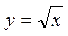 – функция общего вида (ни четная, ни нечетная).
– функция общего вида (ни четная, ни нечетная).
Функция 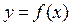 называется периодической, если существует положительное число Т, такое, что
называется периодической, если существует положительное число Т, такое, что 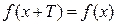 , "
, " 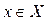 .
.
Примеры. y = tg x – периодическая функция, наименьший период T = π, y = ln x – непериодическая функция.
Значение функции 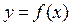 – переменная величина, поэтому можно рассматравать новую функцию с аргументом у: z = g (y), где
– переменная величина, поэтому можно рассматравать новую функцию с аргументом у: z = g (y), где 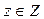 ,
,
т. е. функцию z = g (f (x)). Такая функция называется сложной функцией от х, или суперпозицией функций f и g.
Пример. z = tg(х 2 + 3 x - 1)– суперпозиция функций z = tg у и у = х 2 + 3 x - 1.
Если 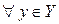 ставится в соответствие единственное значение
ставится в соответствие единственное значение 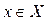 , такое, что
, такое, что 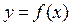 , то говорят, что задана функция
, то говорят, что задана функция 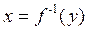 , которую называют обратной по отношению к функции
, которую называют обратной по отношению к функции 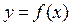 . Функции f и
. Функции f и 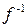 называются взаимно обратными функциями. Если у обратной функции
называются взаимно обратными функциями. Если у обратной функции 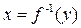 обозначить аргумент буквой х, а функцию – буквой у, то графики взаимно обратных функций
обозначить аргумент буквой х, а функцию – буквой у, то графики взаимно обратных функций 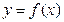 и
и 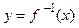 будут симметричны относительно прямой у = х.
будут симметричны относительно прямой у = х.
Пример. y = lg x и y = 10 x – взаимно обратные функции.
Все функции, задаваемые аналитическим способом, можно разбить на два класса: элементарные и неэлементарные. В классе элементарных функций выделяют основные элементарные функции: степенная (у = xn), показательные (y = ax), тригонометрические (y = sin x, y = cos x, y = tg x, y = ctg x), а также обратные к ним (логарифмические, обратные тригонометрические и др.). Элементарными называют функции, полученные из основных элементарных функций при помощи конечного числа операций сложения, вычитания, умножения, деления, а также суперпозиции основных элементарных функций. Все остальные функции относятся к неэлементарным.
Примеры. y = lg(cos x) – элементарная функция, т.к. является суперпозицией основных элементарных функций y = lg x и y = cos x; 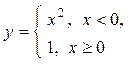 – неэлементарная функция.
– неэлементарная функция.
Нулями функции 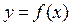 называют точки х, в которых выполнено равенство
называют точки х, в которых выполнено равенство 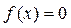 . Нули функции – это абсциссы точек пересечения графика функции с осью Oх.
. Нули функции – это абсциссы точек пересечения графика функции с осью Oх.
Пример. У функции y = lg(x) единственный нуль – точка х = 1.
Функция 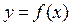 называется монотонно возрастающей на интервале х Î(а; b), если для любых двух точек х 1 и х 2 этого интервала из неравенства х 2 > х 1 следует неравенство
называется монотонно возрастающей на интервале х Î(а; b), если для любых двух точек х 1 и х 2 этого интервала из неравенства х 2 > х 1 следует неравенство 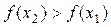 , то есть если любому большему значению аргумента из этого интервала соответствует большее значение функции.
, то есть если любому большему значению аргумента из этого интервала соответствует большее значение функции.
Функция 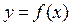 называется монотонно убывающей на интервале х Î(а; b), если для любых двух точек х 1 и х 2 этого интервала из неравенства х 2 > х 1 следует неравенство
называется монотонно убывающей на интервале х Î(а; b), если для любых двух точек х 1 и х 2 этого интервала из неравенства х 2 > х 1 следует неравенство 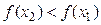 .
.
Промежутки возрастания и убывания функции называются промежутками монотонности функции.
Если функция 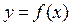 монотонна на интервале хÎ (а; b), то она имеет обратную функцию
монотонна на интервале хÎ (а; b), то она имеет обратную функцию 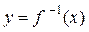 .
.
Пример. Функция y = tg x монотонна на интервале 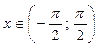 , ее ОЗФ:
, ее ОЗФ: 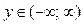 . Она имеет обратную функцию y = arctg x, определенную на интервале
. Она имеет обратную функцию y = arctg x, определенную на интервале 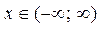 , с ОЗФ:
, с ОЗФ: 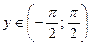 .
.
Точка х 0 называется точкой максимума функции 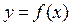 , если существует такая двухсторонняя окрестность точки х 0, что для всякой точки х ¹ х 0 этой окрестности выполняется неравенство
, если существует такая двухсторонняя окрестность точки х 0, что для всякой точки х ¹ х 0 этой окрестности выполняется неравенство 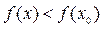 . При этом число
. При этом число 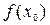 называется максимумом функции
называется максимумом функции 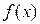 и обозначается y max.
и обозначается y max.
Аналогично, если для всякой точки х ¹ х 0 из некоторой окрестности точки х 0 выполняется неравенство 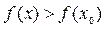 , то х 0 называется точкой минимума, а число
, то х 0 называется точкой минимума, а число 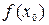 – минимумом функции
– минимумом функции 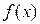 и обозначается y min.
и обозначается y min.
Точки максимумов и минимумов называются точками экстремумов функции, а числа y max и y min называются экстремумами функции.
Пример. Функция y = cos x имеет точки максимумов 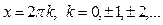 ,
, 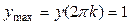 , и точки минимумов
, и точки минимумов 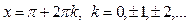 ,
, 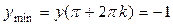 .
.
 2015-01-21
2015-01-21 1055
1055
