Пусть ф-я 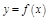 опр. в т.
опр. в т. 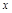 и в нек-й ее окр-ти
и в нек-й ее окр-ти 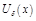 . Дадим арг.
. Дадим арг. 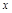 приращение
приращение 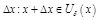 , тогда ф-я получит приращение
, тогда ф-я получит приращение 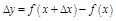 .
.
Опр.1 Производной ф-и 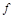 в т
в т 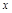 наз. предел отношения приращения ф-и к соответствующему приращению арг., когда последнее стремится к 0:
наз. предел отношения приращения ф-и к соответствующему приращению арг., когда последнее стремится к 0:
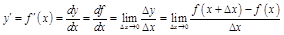 .
.
Пр. 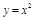
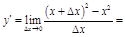
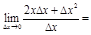
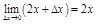 .
.
Опр.2. Правой (левой) производной наз. 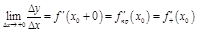
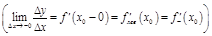 .
.
Т1. Критерий сущ-ния производной в точке: 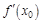 существует
существует 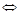
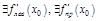 и
и 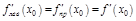 .
.
Опр.3. Ф-я 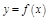 , имеющая конечную производную в
, имеющая конечную производную в
т. 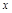 , наз. дифференцируемой в этой точке.
, наз. дифференцируемой в этой точке.
Опр. 4. Если 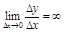 , то говорят, что в т.
, то говорят, что в т. 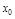 сущ. бесконечная производная.
сущ. бесконечная производная.
Аналогично м. показать, что основные эл. функции диф-мы в т. 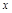 .
.
_______________________________________________________
Т.2. О связи диф-ти и непрерывности функции в точке: Если ф-я 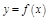 диф-ма в т.
диф-ма в т. 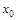 , то она непр. в этой точке.
, то она непр. в этой точке.
Д-во: 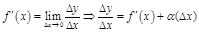 , где
, где 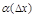 – б.м. при
– б.м. при 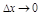 , тогда
, тогда 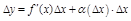
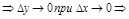
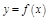 непр.
непр. 
Зам. Дифференцируемость 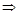 непрерывность,
непрерывность,
непрерывность 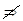 дифференцируемость.
дифференцируемость.
ПР. 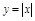 – непр., но не диф. в т.
– непр., но не диф. в т. 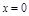 ,
,
т.к. 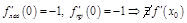 .
.
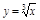 непр., но не диф. в т.
непр., но не диф. в т. 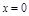 .
.
 2015-01-21
2015-01-21 351
351







