Опр. Ф-я наз-ся строго возрастающей (убывающей) на промежутке 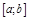 , если
, если 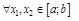
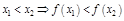
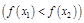 .
.
Опр. Строго возрастающая или строго убывающая ф-я
наз-ся строго монотонной на 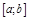 .
.
Т.4. О производной обратной функции: Если ф-я 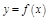 строго монотонна на интервале
строго монотонна на интервале 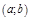 и имеет ненулевую производную
и имеет ненулевую производную 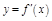 в некоторой
в некоторой
т. 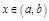 , то:
, то:
1) 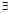 обратная ф-я
обратная ф-я 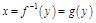 ;
;
2) 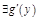 в соответствующей точке;
в соответствующей точке;
3) 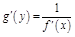 или
или 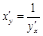 .
.
Геометрическая интерпретация:
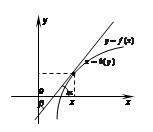
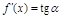 ,
, 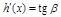
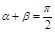
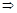
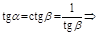
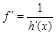 .
.
Д-во. 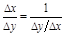 ;
; 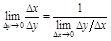 ; т.к.
; т.к. 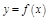 - диф.
- диф. 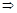 - непр.
- непр. 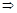
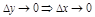 .
.
ПР. 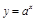 ,
, 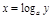 ,
, 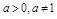 ;
; 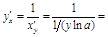
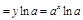 .
.
ПР. 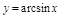 ,
, 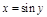 ,
, 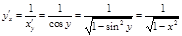 .
.
 2015-01-21
2015-01-21 287
287








