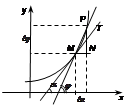 Опр.5. Касательной к кривой графика функции
Опр.5. Касательной к кривой графика функции 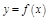 в т.
в т. 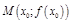 наз-ся предельное положение
наз-ся предельное положение 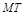 секущей
секущей 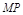 , когда т.
, когда т. 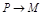 вдоль кривой (т.е. угол
вдоль кривой (т.е. угол 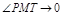 при
при 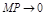 ).
). 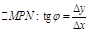 ,
, 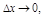
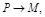
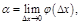
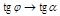 ,
, 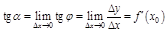 .
.
Зам. 
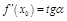 – угловой коэффициент касательной к графику ф-и
– угловой коэффициент касательной к графику ф-и 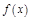 в
в 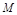
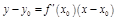 – уравнение касательной к графику функции
– уравнение касательной к графику функции 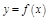 в точке
в точке 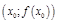 , где
, где 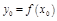 .
.
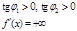 ,
, 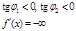 ,
, 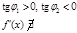 ,
, 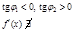 .
.
Опр.6. Углом между кривыми наз. угол между касат-ми, проведенными к данным кривым в т. их пересечения.
Физический смысл производной.
Пусть т. движется по прямой, закон движения. 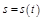 . Дадим приращение
. Дадим приращение 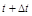 , тогда
, тогда 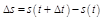 ,
, 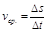 ,
, 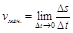
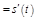 .
.
 2015-01-21
2015-01-21 308
308








