Опр. Ф-ция 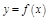 достигает в т.
достигает в т. 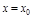 локального максимума (минимума), если
локального максимума (минимума), если 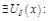
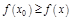
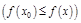
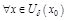 .
.
Опр. Лок. минимум и лок. максимум ф-и наз-ся локальным экстремумом ф-ции.
Т. 7. Ролля (О корнях производной): Пусть:
1) 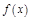 непрерывна на
непрерывна на 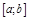 ;
;
2) 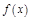 диф-ма на
диф-ма на 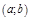 ;
;
3) 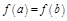 ,
,
тогда 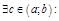
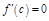 .
.
Д-во. Т.к. 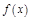 непр. на
непр. на 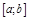
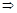
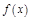 (по т. Вейерштрасса) достигает своего наиб. и наим. значения:
(по т. Вейерштрасса) достигает своего наиб. и наим. значения:
_______________________________________________________
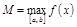 ,
, 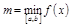 . Рассмотрим два случая.
. Рассмотрим два случая.
а) 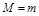 , то
, то 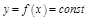
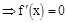
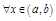 ;
;
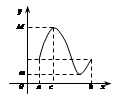 б)
б) 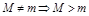 . Пусть
. Пусть 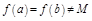 или
или 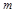
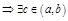 :
: 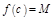 . Док-м, что
. Док-м, что 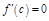 .
. 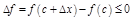 для
для 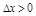 и
и 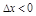
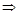
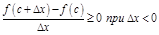 ,
, 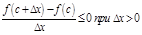 ,
, 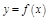 – дифференцируемая в т. c, следовательно
– дифференцируемая в т. c, следовательно 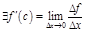 . Т.о., имеем
. Т.о., имеем 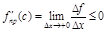 ,
, 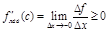 . Если
. Если 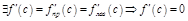 .
.
Геом. смысл: В т. лок. экстремума касательная к графику 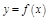 параллельна Ox.
параллельна Ox.
Т. 8. Лагранжа (о конечных приращениях): Пусть 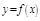
1) непр. на 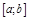 ;
;
2) диф. на 
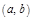 ,
,
тогда 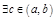 :
: 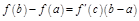 .
.
 Геом. смысл:
Геом. смысл: 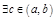 , касательная в к-й парал. хорде AB.
, касательная в к-й парал. хорде AB.
Д-во. Введем функцию 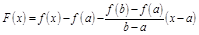 , к-я: а) непр. на
, к-я: а) непр. на 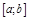 , т.к.
, т.к. 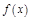 непр.; б) диф. на
непр.; б) диф. на 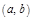 т.к. …; в)
т.к. …; в) 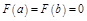
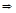 по т. Ролля
по т. Ролля 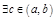 :
: 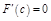 , и
, и 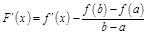 .
. 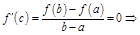
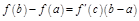
 .
.
Зам. Пусть 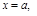
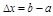
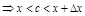
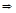
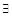
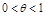 :
: 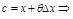
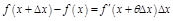 – ф-ла Лагранжа.
– ф-ла Лагранжа.
Т.9. Коши (об отношении конечных приращений): Пусть:
1) 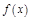 и
и 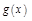 непр. на
непр. на 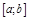 ;
;
2) 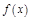 и
и 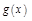 диф. на
диф. на 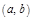 ;
;
3) 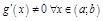 ,
,
тогда 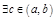 :
: 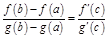 .
.
Д-во. 1) 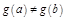 , иначе по т. Ролля
, иначе по т. Ролля 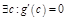 ;
;
2) 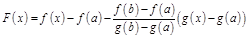 уд-ет усл-ю т.Ролля
уд-ет усл-ю т.Ролля 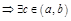 :
: 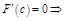
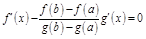
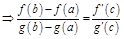 .
. 
_______________________________________________________
 2015-01-21
2015-01-21 278
278







