Расчет свободной энергии Гиббса и энтропии вещества при давлении, отличном от давления при стандартных условиях

Молярные энтальпия 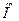, теплоемкости 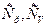и внутренняя энергия 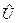зависят только от температуры: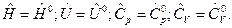

Молярные энтропия 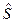, свободная энергия Гиббса 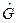, свободная энергия Гельмгольца 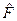зависят от температуры и давления.

Установим связь между величинами: 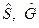и их значениями при стандартном состоянии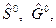 которые определяются с использованием справочных материалов.

Получим сначала выражение для свободной энергии Гиббса. Из объединенного выражения 1 –го и 2 –го законов термодинамики для простой, закрытой ТС и для обратимых процессов для 1 моля вещества имеем:

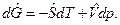
При T= const (dT = 0) получаем 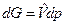, где 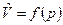. Откуда после интегрирования для конечного процесса в диапазоне давлений от р ⁰ до р имеем

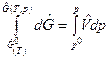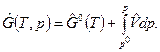, или (1)

где 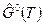-молярная свободная энергия Гиббса при р ⁰=1физ.атм, 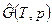- то же при давлении 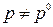. Зависимость (1) справедлива для газообразных и конденсированных веществ при Т =const.

Для идеального газа, 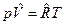. Следовательно, 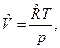а интеграл в (1) будет равен 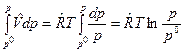. Обозначив через 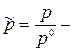безразмерное давление; где р ⁰ = 101325Па; ~ тильда, получим для идеального газа формулу для расчета свободной энергии Гиббса при давлении р≠р ⁰:

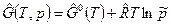, (2)

Если вещество находится в газовой смеси, то для i -ого компонента смеси идеальных газов имеем:

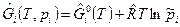, (3)

где нормированное парциальное давление 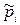и нормированное давление смеси 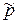связаны соотношением 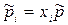, учитывающим молярную долю 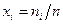i-го газа, 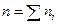, а давление смеси газов определяется законом Дальтона 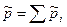.Для получения формулы для расчета 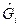, выраженной через молярные доли, представим формулу (3) в виде:

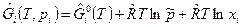(4)

Обозначим 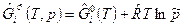- молярную свободную энергию Гиббса i -го газа при давлении смеси. Тогда получим

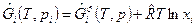. (5)

Молярные свободные энергии Гиббса конденсированных веществ от давления не зависят, поскольку можно пренебречь их объемами по сравнению с объемами газообразных компонентов. Тогда формула для расчета 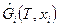конденсированных веществ примет вид:

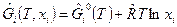, (6)

где х_i – молярная доля i -го вещества относительно фазы, в которой оно находится(к числу молей своей фазы), 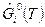— молярная свободная энергия Гиббса чистого конденсированного вещества, при p=p ⁰=101325Па.

Влияние давления на энтропию может быть определено из выражения для молярной свободной энергии Гиббса для i -го компонента идеального газа при давлении p ≠ p ⁰

,

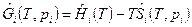из которого следует, что

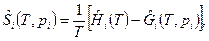(7)

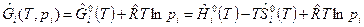где . (8)

После подстановки (8) в (7) и учитывая, что 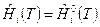, получим:

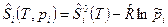. (9)

Для i-го компонента конденсированного вещества по аналогии с выражением (9) можно получить формулу для расчета энтропии при p ≠ p ⁰

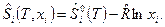(10)

Величина 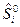- берется из справочника при р⁰ =101325 Па.