Изохорный процесс – это процесс сообщения или отнятия теплоты от газа при постоянном объеме v=const.
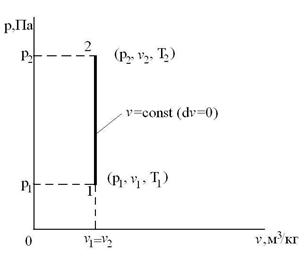
Этот процесс используется как подготовительный процесс в циклах.
Соотношение между параметрами для конечного участка процесса 1-2 определяется законом Шарля: 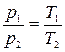 , который следует из уравнений состояния для точек 1 и 2:
, который следует из уравнений состояния для точек 1 и 2: 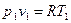 и
и 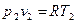 при
при 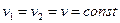 .
.
Поскольку работа расширения в этом процессе равна нулю: 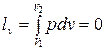 , т.к.
, т.к. 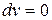 , то из уравнения 1-го закона термодинамики следует, что:
, то из уравнения 1-го закона термодинамики следует, что:
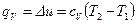 .
.
Таким образом, подведенная к газу в изохорном процессе теплота целиком идет на увеличение его внутренней энергии. Для ТП 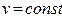 коэффициент распределения теплоты
коэффициент распределения теплоты 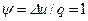 , теплоемкость
, теплоемкость 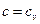 и показатель политропы:
и показатель политропы:
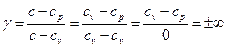 .
.
График распределения энергетических составляющих уравнения 1-го закона термодинамики в изохорном процессе имеет вид:
Изобарный процесс – это процесс сообщения или отнятия теплоты от газа при постоянном давлении р=const.
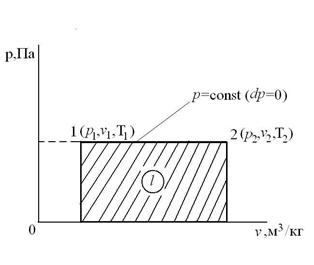
Соотношение между параметрами в процессе р=const: 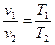 - закон Гей-Люссака, т.к.:
- закон Гей-Люссака, т.к.: 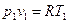 ,
, 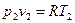 и
и 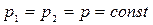 .
.
Работа расширения 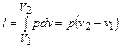 . Т.к.
. Т.к. 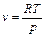 , то
, то 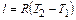 .
.
Следовательно, удельная газовая постоянная R - это работа, совершаемая 1кг газа в процессе p=const при его нагревании на один градус. Размерность R: Дж/кгК. Уравнение 1-го закона термодинамики в этом случае имеем вид:
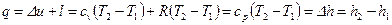 .
.
Таким образом, вся теплота, подведенная к газу в изобарном процессе, расходуется на увеличение его энтальпии.
Коэффициент распределения теплоты в процессе р=const равен:
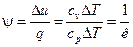 ,
, 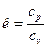 .
.
Теплоемкость с=ср и показатель политропы
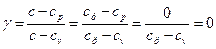 .
.
График распределения энергетических составляющих 1-го закона термодинамики в изобарном процессе имеет вид:
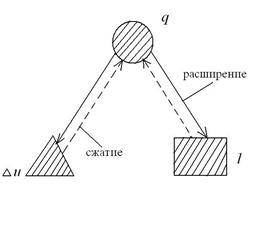
В T-s координатах взаимное положение изобары и изохоры имеет вид:
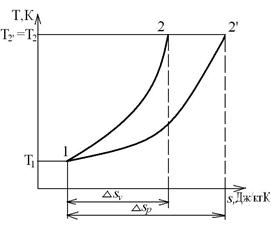
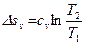 ,
, 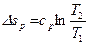 , т.е. изобара более пологая логарифмическая кривая в T-s координатах, чем изохора.
, т.е. изобара более пологая логарифмическая кривая в T-s координатах, чем изохора.
Изотермический процесс – это процесс сообщения или отнятия теплоты от газа при постоянной температуре
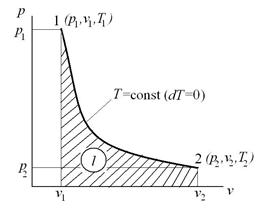
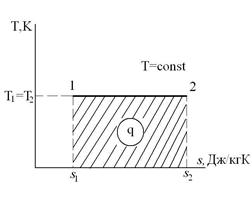
При Т=const из уравнения состояния  имеем:
имеем: 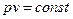 - это уравнение изотермического процесса является уравнением равнобокой гиперболы.
- это уравнение изотермического процесса является уравнением равнобокой гиперболы.
Тогда 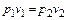 , и
, и 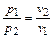 - закон Бойля-Мариотта.
- закон Бойля-Мариотта.
Из уравнения 1-го закона термодинамики 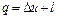 при
при 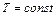 имеем:
имеем:
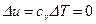 и q=l, т.е. вся теплота, сообщаемая газу в изотермическом процессе, целиком идет на работу расширения газа.
и q=l, т.е. вся теплота, сообщаемая газу в изотермическом процессе, целиком идет на работу расширения газа.
Изменение энтальпии в процессе T=const равно:
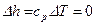 .
.
Работа расширения 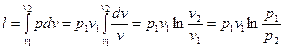 .
.
Коэффициент распределения теплоты
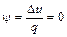 .
.
Тогда теплоемкость 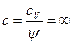 и показатель политропы для процесса T=const будет равен
и показатель политропы для процесса T=const будет равен 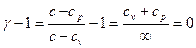 , т.е.
, т.е. 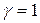 .
.
График распределения энергии в процессе T=const имеет вид:
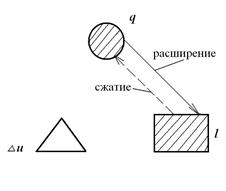
Адиабатный процесс – это процесс, протекающий без внешнего теплообмена, т.е. q =0 и 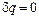 (на конечном и бесконечно малом участке процесса).
(на конечном и бесконечно малом участке процесса).
Если записать для этого случая уравнения 1-го закона термодинамики в виде:
1. 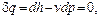 или
или 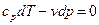 ,
,
2. 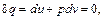 или
или 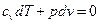 , то после деления (1) на (2) получим:
, то после деления (1) на (2) получим:
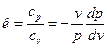 - показатель адиабаты.
- показатель адиабаты.
Тогда после интегрирования выражения 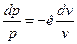 для конечного процесса 1-2 будем иметь
для конечного процесса 1-2 будем иметь 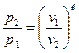 , или
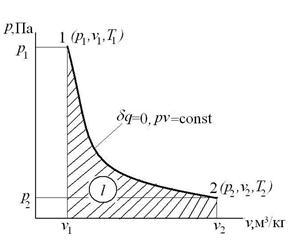
, или 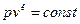 - это есть уравнение адиабатного процесса в p-v -координатах, которое является уравнением неравнобокой гиперболы.
- это есть уравнение адиабатного процесса в p-v -координатах, которое является уравнением неравнобокой гиперболы.
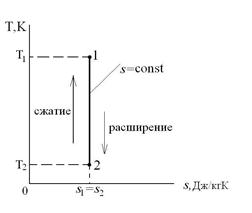
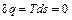 , т.к. Т
, т.к. Т 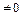 , то ds =0 и s=const. Таким образом, адиабатный процесс с идеальным газом есть изоэнтропийный процесс.
, то ds =0 и s=const. Таким образом, адиабатный процесс с идеальным газом есть изоэнтропийный процесс.
Соотношения между параметрами состояния в этом процессе:
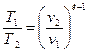 и
и 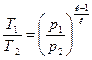 , а график распределения энергии в процессе имеет вид:
, а график распределения энергии в процессе имеет вид:
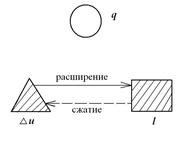
Из уравнения 1-го закона термодинамики следует, что 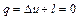 , т.е.
, т.е. 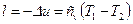 . Таким образом, работа расширения в адиабатном процессе совершается за счет уменьшения внутренней энергии газа, а его температура уменьшается
. Таким образом, работа расширения в адиабатном процессе совершается за счет уменьшения внутренней энергии газа, а его температура уменьшается 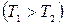 .
.
Работа расширения по аналогии с политропным процессом будет равна:
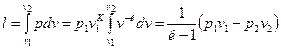 ,
,
или 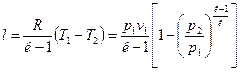 .
.
Коэффициент распределения теплоты в процессе q =0:
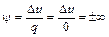 , а теплоемкость адиабатного процесса
, а теплоемкость адиабатного процесса 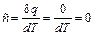 .
.
Показатель адиабаты 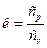 для одноатомных газов равен к =1,66, для двухатомных к =1,4 и для трехатомных к =1,3.
для одноатомных газов равен к =1,66, для двухатомных к =1,4 и для трехатомных к =1,3.
 2015-01-21
2015-01-21 4576
4576








