12.1. Вывод уравнения политропного процесса в р-v координатах
Политропные процессы – это равновесные, обратимые процессы, которые протекают при постоянной теплоемкости c= const. Многие реальные процессы могут быть приближенно описаны уравнениями для политропных процессов.
Каждый политропный термодинамический процесс (ТП) имеет вполне определенный, присущий ему характер распределения энергетических составляющих, входящих в уравнение первого закона термодинамики: 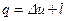 , Дж/кг. Это распределение энергетических составляющих будем интерпретировать графически. Например, для процесса V=const имеем:
, Дж/кг. Это распределение энергетических составляющих будем интерпретировать графически. Например, для процесса V=const имеем:
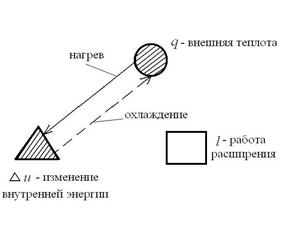
Штриховка на рисунке означает изменение данной энергетической составляющей, а стрелка – направление ее изменения.
Политропный процесс – это процесс изменения состояния рабочего тела, в котором во внутреннюю энергию в течение всего процесса превращается одна и та же доля количества внешней теплоты:
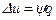 , Дж/кг, где
, Дж/кг, где 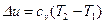 .
.
При этом на совершение внешней механической работы приходится доля теплоты, равная:
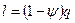 , Дж/кг,
, Дж/кг,
где 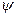 - коэффициент распределения теплоты в политропном процессе.
- коэффициент распределения теплоты в политропном процессе.
Теплота, сообщенная газу в бесконечно малом политропном процессе, равна:
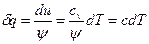 , Дж/кг
, Дж/кг
или для конечного процесса 1-2: 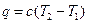 .
.
Таким образом, получим теплоемкость политропного процесса: 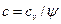 , Дж/кгК.
, Дж/кгК.
Зная значение коэффициента 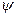 в политропном процессе, можно определить теплоемкость c, теплоту q, изменение внутренней энергии
в политропном процессе, можно определить теплоемкость c, теплоту q, изменение внутренней энергии 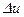 и работу расширения (сжатия) l.
и работу расширения (сжатия) l.
Для вывода уравнения политропного процесса в p-v координатах используем уравнения первого закона термодинамики, выраженные через энтальпию и внутреннюю энергию:
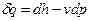 , (1)
, (1)
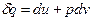 , (2)
, (2)
или
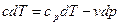 , (3)
, (3)
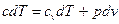 . (4)
. (4)
Отсюда имеем:
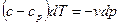 , (5)
, (5)
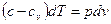 . (6)
. (6)
Разделив почленно уравнение (5) на уравнение (6), имеем:
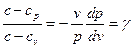 , (7)
, (7)
где 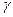 - показатель политропного процесса, который не изменяется в течение всего данного ТП. Из уравнения (7) имеем:
- показатель политропного процесса, который не изменяется в течение всего данного ТП. Из уравнения (7) имеем:
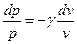 .
.
Тогда после интегрирования для конечного участка процесса 1-2 получим:
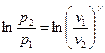 , или после потенцирования:
, или после потенцирования:
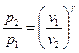 , или
, или 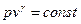 . (8)
. (8)
Это уравнение политропного процесса в координатах p-v. Показатель политропного процесса может иметь любое значение в интервале 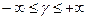 .
.
Из выражения (7)можно получить формулу для расчета теплоемкости политропного процесса
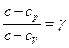 , или
, или 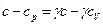 . Отсюда имеем
. Отсюда имеем 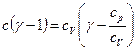 , или
, или 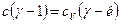 , где к=сp/сV – показатель адиабатного процесса. Окончательно имеем:
, где к=сp/сV – показатель адиабатного процесса. Окончательно имеем:
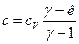 . (9)
. (9)
Таким образом, теплоемкость политропного процесса зависит от показателя политропы 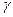 . Используя термическое уравнение состояния для идеального газа
. Используя термическое уравнение состояния для идеального газа  и уравнение (8), можно получить соотношения между параметрами для конечного процесса 1-2:
и уравнение (8), можно получить соотношения между параметрами для конечного процесса 1-2:
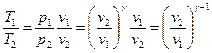 . (10)
. (10)
Учитывая, что 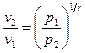 , имеем:
, имеем:
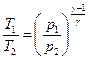 . (11)
. (11)
12.2. Расчет теплоты, работы, изменений внутренней энергии, энтальпии и энтропии. Уравнение политропных процессов в T-s координатах
Коэффициент распределения теплоты равен: 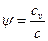 . Поскольку
. Поскольку 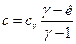 , то коэффициент
, то коэффициент
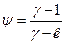 . (12)
. (12)
Тогда изменение внутренней энергии в ТП 1-2 и теплота процесса могут быть рассчитаны по формулам:
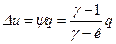 , (13)
, (13)
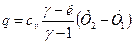 , (14)
, (14)
а изменение энтальпии по формуле:
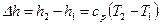 . (15)
. (15)
Работа расширения в политропном процессе 1-2 равна:
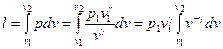 .
.
После интегрирования, учитывая, что 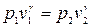 , имеем различные выражения для расчета работы расширения:
, имеем различные выражения для расчета работы расширения:
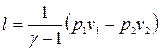 , (16)
, (16)
или
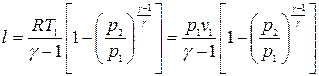 , (17)
, (17)
или
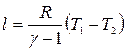 . (18)
. (18)
Расчет располагаемой работы l 0 проводятся, используя следующее выражение:
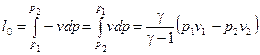 , (19)
, (19)
Зная l 0 по (19) и l по (16) можно определить показатель политропы 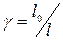 . Это один из способов опытного определения величины
. Это один из способов опытного определения величины 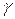 . С другими способами студенты будут ознакомлены при выполнении лабораторных работ.
. С другими способами студенты будут ознакомлены при выполнении лабораторных работ.
Для расчета изменения удельной энтропии в политропном процессе используем объединенное выражение 1-го и 2-го законов термодинамики для обратимых процессов:
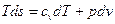 . (20)
. (20)
или 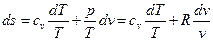 .
.
После интегрирования для конечного процесса 1-2 имеем:
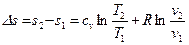 . (21)
. (21)
Если учесть, что 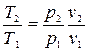 и
и  , то получим:
, то получим:
 . (22)
. (22)
Выразим 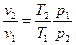 и подставим в (22).
и подставим в (22).
Тогда 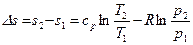 . (23)
. (23)
Уравнение политропного процесса в координатах T-s будет иметь вид:
 - для бесконечно малого ТП. После интегрирования получим:
- для бесконечно малого ТП. После интегрирования получим:
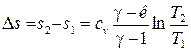 . (24)
. (24)
Зная показатель политропы 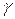 , можно рассчитать величину
, можно рассчитать величину 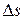 и построить данный ТП в T-s координатах. Из соотношений для политропных процессов вытекают, как частные случаи соотношения и уравнения изохорного, изобарного, изотермического и адиабатного процессов.
и построить данный ТП в T-s координатах. Из соотношений для политропных процессов вытекают, как частные случаи соотношения и уравнения изохорного, изобарного, изотермического и адиабатного процессов.
 2015-01-21
2015-01-21 2434
2434








