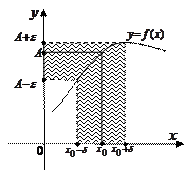Предел функции

Число 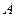называется пределом последовательности 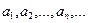, если для любого 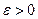существует натуральное число 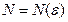такое, что 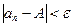при .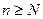

В случае, если последовательность 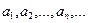имеет своим пределом число 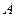, говорят также, что последовательность 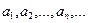сходится (или стремится) к числу 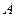, и обозначают этот факт так: .

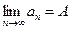Если последовательность не имеет предела, то говорят, что она расходится.

Пример 6.14. Используя определение предела, докажите, что последовательность 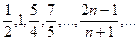сходится к числу 2.

Обозначив 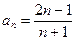, выберем произвольное число 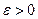. Тогда 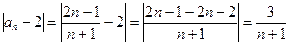и неравенство 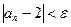будет выполнено тогда, когда 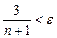, т.е. 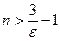. Положив 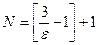(где 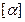означает целую часть 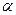), получим, что для всех 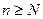справедливо неравенство 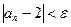. В соответствии с определением предела это и означает, что .

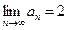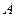Число называется пределом функции 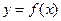в точке 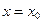, если для любого 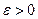существует 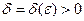такое, что при 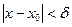выполняется неравенство 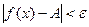. Это кратко записывается в виде .

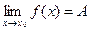Если 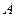есть предел 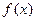в точке 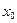, то на графике это иллюстрируется следующим образом. Так как из неравенства 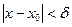следует неравенство 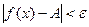, то это значит, что для всех 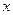, отстоящих от 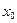не далее чем 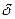, точка 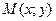графика функции 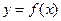лежит внутри полосы шириной 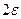, ограниченной прямым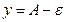и и 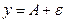. Очевидно, что с уменьшением 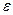величина 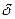также уменьшается.