
 Любое изменение независимой переменной
Любое изменение независимой переменной 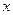 , равное разности
, равное разности 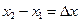 , называется приращением этой переменной.
, называется приращением этой переменной.
 Разность
Разность 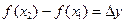 называется приращением функции на отрезке
называется приращением функции на отрезке 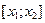 или
или 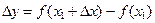 , где
, где 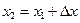 .
.
Производной функции 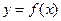 называется предел отношения приращения функции
называется предел отношения приращения функции 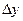 к приращению аргумента
к приращению аргумента 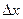 при условии, что приращение аргумента стремится к нулю, т.е.
при условии, что приращение аргумента стремится к нулю, т.е.

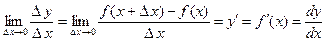 .
.
Функция, имеющая в данной точке конечную производную, называется дифференцируемой в этой точке.
Пример 7.1. Пользуясь определением, найдите производную функции 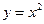 .
.
 Придадим аргументу
Придадим аргументу 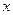 приращение
приращение 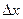 . Тогда соответствующее приращение
. Тогда соответствующее приращение 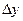 функции будет иметь вид
функции будет иметь вид
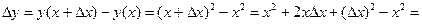
 .
.
Отсюда 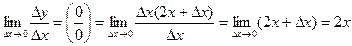
 Таким образом,
Таким образом, 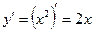 .
.
 Теорема. Если функция дифференцируема в некоторой точке
Теорема. Если функция дифференцируема в некоторой точке 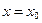 , то она непрерывна в этой точке.
, то она непрерывна в этой точке.
 Однако, обратное утверждение вообще говоря не верно. Существуют непрерывные, но не дифференцируемые функции. Например,
Однако, обратное утверждение вообще говоря не верно. Существуют непрерывные, но не дифференцируемые функции. Например, 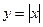 при
при 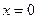 .
.

 2015-01-21
2015-01-21 386
386








