Функции нескольких переменных

Пусть 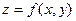— функция двух переменных. Нададим независимой переменной 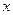приращение 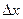, оставляя при этом переменную 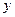неизменной. Тогда 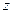получит приращение

,

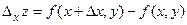которое называется частным приращением 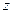по .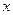

Аналогично, если независимой переменной 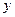нададим приращение 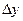, оставляя при этом неизменной переменную 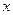, то 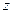получит приращение

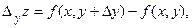
называемое частным приращением 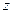по .

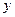Частной производной по 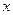от функции 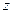называется предел отношения частного приращения 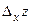к приращению 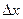при стремлении 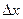к нулю.

Таким образом по определению,

.

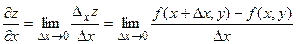Эта производная обозначается одним из символов

.

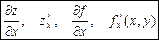Аналогично определяется частная производная от функции 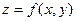по переменной :

.

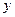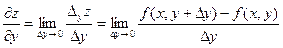Она обозначается одним из символов

.

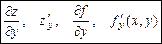Пример 8.3. Найдите значения частных производных функции 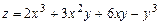в точке .

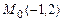Считая 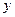постоянной и дифференцируя 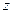, как функцию переменной 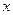, находим частную производную по :

.

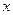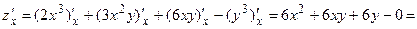
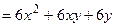Вычислим значение этой производной в точке : .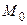

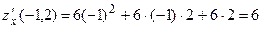Считая 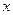постоянной и дифференцируя 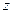, как функцию 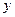, находим частную производную по :

.

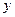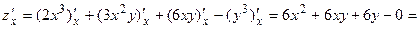
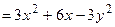Вычислим значение производной в точке :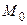

.

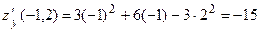§ 3. Полный дифференциал