2015-01-21
435
 |
Полное приращение функции двух переменных.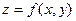 
в точке 
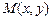определяется формулой
,
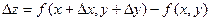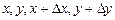принадлежат области определения функции.
Предположим, что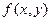 
в точке 
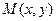имеет непрерывные частные производные.
Полным дифференциалом функции 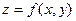называется главная часть полного приращения 
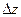, линейная относительно приращений аргументов 
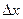и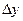 
. Обозначается символом 
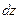или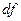 
и вычисляется по формуле
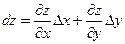. (8.1)
Так как дифференциалы независимых переменных совпадают с их приращениями, т.е.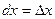 
, 
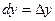, то формулу (8.1) можно записать в виде:
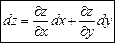. (8.2)
Пример 8.5. Найти полный дифференциал функции
.
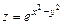Находим частные производные функции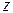 
:
, 
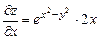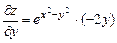
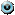Тогда, в соответствии с формулой (8.2), полный дифференциал запишем в виде 
.
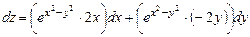Пример 8.6 Найти полный дифференциал функции
.
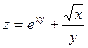Находим частные производные функции :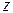
, 
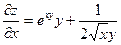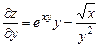
Тогда полный дифференциал запишем в виде
.
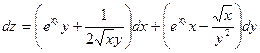§ 4. Частные производные и
