Физическая система считается идеальной, если она
1. физически осуществима;
2. имеет постоянные параметры;
3. устойчива;
4. линейна.
Основные свойства такой идеальной системы описываются ее импульсной характеристикой (весовой функцией), которая представляет собой реакцию системы на входное возмущение в виде дельта-функции.
Дельта-функция – это математическая идеализация предельно короткого импульсного сигнала. Иными словами, это импульс бесконечно большой амплитуды и бесконечно малой длительности, площадь которого равна единице. Дельта-функция определяется следующими соотношениями:
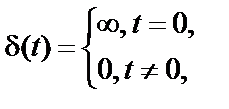
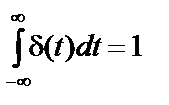 . (2.1)
. (2.1)
На графике дельта-функцию условно изображают в виде утолщения на оси ординат (рисунок 2.2).
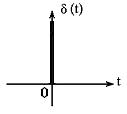
Рисунок 2.2 – Дельта-функция
Зная импульсную характеристику системы, можно рассчитать реакцию системы на входной сигнал произвольной формы, используя интеграл свертки (интеграл Дюамеля):
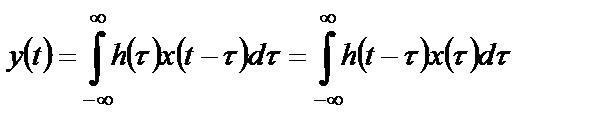 , (2.2)
, (2.2)
где 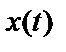 – входной сигнал;
– входной сигнал;
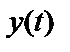 – выходной сигнал;
– выходной сигнал;
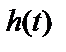 – импульсная характеристика;
– импульсная характеристика;
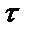 – промежуток времени (время задержки), необходимый для ответной реакции системы на входное воздействие.
– промежуток времени (время задержки), необходимый для ответной реакции системы на входное воздействие.
Физически осуществимая система не может реагировать на возмущение до тех пор, пока оно не поступило на вход системы. Это означает, что
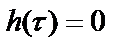 при
при 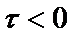 . (2.3)
. (2.3)
Интеграл свертки для физически осуществимой системы примет вид
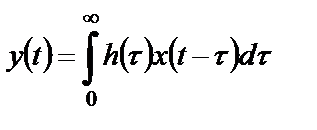 . (2.4)
. (2.4)
Физическая система имеет постоянные параметры, если ее импульсная характеристика не зависит от момента поступления вынуждающей силы на вход системы, т.е.
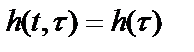 при
при 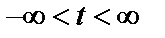 . (2.5)
. (2.5)
Физическая система называется устойчивой, если при нулевом входном сигнале выходной сигнал затухает при любых начальных условиях. Это требование равносильно требованию затухания импульсной характеристики, т.е.
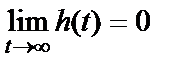 . (2.6)
. (2.6)
Линейная система обладает свойствами аддитивности и однородности.
Пусть входные процессы 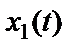 и
и 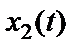 генерируют выходные процессы
генерируют выходные процессы 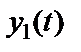 и
и 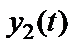 соответственно.
соответственно.
Система называется аддитивной, если входной процесс 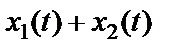 генерирует на выходе системы процесс
генерирует на выходе системы процесс 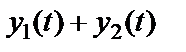 , т.е. отклик системы на сумму воздействий равен сумме откликов на каждое из воздействий.
, т.е. отклик системы на сумму воздействий равен сумме откликов на каждое из воздействий.
Система называется однородной, если входному процессу 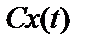 соответствует выходной процесс
соответствует выходной процесс 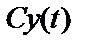 , где
, где 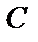 – произвольная постоянная. Другими словами, свойство однородности означает, что система пропорционально реагирует на изменение входного воздействия.
– произвольная постоянная. Другими словами, свойство однородности означает, что система пропорционально реагирует на изменение входного воздействия.
На практике линейность относится к числу наиболее редко выполняемых свойств. Однако если изучаемая система не является сильно нелинейной, то рассматриваемые методы корреляционного и спектрального анализа приведут к вполне осмысленным результатам, описывающим наилучшие линейные приближения для исследуемых систем.
 2015-01-22
2015-01-22 632
632








