1. Точка движется по окружности радиусом R=1,2 м. Уравнение движения точки 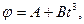 где А=0,5 рад/с; В=0,2 рад/с3. Определить тангенциальное аτ, нормальное аn и полное а ускорения точки в момент времени t =4 с.
где А=0,5 рад/с; В=0,2 рад/с3. Определить тангенциальное аτ, нормальное аn и полное а ускорения точки в момент времени t =4 с.
2. Определить скорость υ и полное ускорение а точки в момент времени t =2 с, если она движется по окружности радиусом R =1 м согласно уравнению ξ=At+Bt3, где А=8 м/с; В=-1 м/с3; ξ – криволинейная координата, отсчитанная от некоторой точки, принятой за начальную, вдоль окружности.
3. По прямой линии движутся две материальные точки согласно уравнениями: 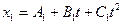 и
и 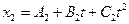 , где А 1=10 м; В 1=1 м/с; С 1=-2 м/с2; А 2=3 м; В 2=2 м/с; С 2=0,2 м/с2. В какой момент времени τ скорости этих точек будут одинаковы? Найти ускорение а 1 и а 2 этих точек в момент t =3 с.
, где А 1=10 м; В 1=1 м/с; С 1=-2 м/с2; А 2=3 м; В 2=2 м/с; С 2=0,2 м/с2. В какой момент времени τ скорости этих точек будут одинаковы? Найти ускорение а 1 и а 2 этих точек в момент t =3 с.
4. Определить полное ускорение а в момент t =3 с точки, находящейся на ободе колеса радиусом R =0,5 м, вращающегося согласно уравнению 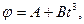 где А =2 рад/с; В =0,2 рад/с3.
где А =2 рад/с; В =0,2 рад/с3.
5. Точка движется по окружности радиусом R =8 м. В некоторой момент времени нормальное ускорение точки аn= 4 м/с2, вектор полного ускорения а образует в этот момент с вектором нормального ускорения аn угол α=600. Найти скорость υ и тангенциальное ускорение аτ точки.
6. Точка движется по прямой согласно уравнению 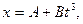 где А =6 м/с; В = –0,125 м/с3. Определить среднюю путевую скорость <υ> точки в интервале времени от t1 =2 с до t2=6 с.
где А =6 м/с; В = –0,125 м/с3. Определить среднюю путевую скорость <υ> точки в интервале времени от t1 =2 с до t2=6 с.
7. Материальная точка движется прямолинейно. Уравнение движения имеет вид х=Аt+Вt3, где А =3 м/с; В =0,06 м/с3. Найти скорость υ и ускорение а точки в моменты времени t=0 и t2=3 с. Каковы средние значения скорости <υx> и ускорения < а x> за первые 3 с движения?
8. Диск радиусом R =0,2 м вращается согласно уравнению φ=А+Вt+Сt3, где А =3 рад; В = – 1 рад/с; С =0,1 рад/с3. Определить тангенциальное аτ, нормальное аn и полное а ускорения точек на окружности диска для момента времени t = 10с.
9. С высоты h =2 м на стальную плиту свободно падает шарик массой т =200 г и подпрыгивает на высоту h 1=0,5 м. Определить импульс р, полученный шариком при ударе.
10. При горизонтальном полете со скоростью υ =250.м/с снаряд массой т =8 кг разорвался на две части, Большая часть массой т 1=6 кг получила скорость u 1=400 м/с в направлении полета снаряда. Определить модуль и направление скорости u 2 меньшей части снаряда.
11. Орудие, жестко закрепленное на железнодорожной платформе, производит выстрел вдоль полотна железной дороги под углом α=300 к линии горизонта. Определить скорость u2 отката платформы, если снаряд вылетает со скоростью u 1=480 м/с. Масса платформы с орудием и снарядами т2 =18 т, масса снаряда т1= 60 кг.
12. Определить импульс р, полученный стенкой при ударе о нее шарика массой т =300 г, если шарик двигался со скоростью υ=8 м/с под углом α=600 к плоскости стенки. Удар о стенку считать упругим.
13. Снаряд, летевший со скоростью υ=400 м/с, разорвался на два осколка. Меньший осколок, масса которого составляет 40 % от массы снаряда, полетел в противоположном направлении со скоростью и1 = 150 м/с. Определить скорость и2 большего осколка.
14. По небольшому куску мягкого железа, лежащему на наковальне массой т 1=300 кг, ударяет молот массой т 2=8 кг. Определить к. п. д. η удара, если удар неупругий. Полезной считать энергию, затраченную на деформацию куска железа.
15. Шар массой т 1=1 кг движется со скоростью υ1=4 м/с и сталкивается с шаром массой т 2=2 кг, движущимся навстречу ему со скоростью υ2=3 м/с. Каковы скорости и 1 и и 2 шаров после удара? Удар считать абсолютно упругим, прямым, центральным.
16. Шар массой т1 =3 кг движется со скоростью υ1=2 м/с и сталкивается с покоящимся шаром массой т 2=5 кг. Какая работа будет совершена при деформации шаров? Удар считать абсолютно неупругим, прямым, центральным.
17. Определить к. п. д. η неупругого удара бойка массой т 1=0,5 т, падающего на сваю массой т 2=120 кг. Полезной считать энергию, затраченную на вбивание сваи.
18. Шар массой т1 =4 кг движется со скоростью υ1=5 м/с и сталкивается с шаром массой т 2=6 кг, который движется ему навстречу со скоростью υ2=2 м/с. Определить скорости и 1 и и 2 шаров после удара. Удар считать абсолютно упругим, прямым, центральным.
19. На покоящийся шар массой т1 =5 кг налетает со скоростью υ2=5 м/с шар массой т 2=3 кг. Направление движения второго шара изменилось на угол α=450. Определить скорости и 1 и и 2 шаров после удара, считая шары абсолютно упругими.
20. Атом распадается на две части массами 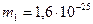 кг и
кг и 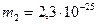 кг. Определить кинетические энергии Т1 и Т2 частей атома, если их общая кинетическая энергия Т =2,2∙10-11 Дж. Кинетической энергией и импульсом атома до распада пренебречь.
кг. Определить кинетические энергии Т1 и Т2 частей атома, если их общая кинетическая энергия Т =2,2∙10-11 Дж. Кинетической энергией и импульсом атома до распада пренебречь.
21. Определить работу растяжения двух соединенных последовательно пружин жестокостями k 1=400 Н/м и k 2=250 Н/м, если первая пружина при этом растянулась на ∆ l =2 см.
22. Из ствола автоматического пистолета вылетела пуля массой т 1=10 г со скоростью υ=300 м/с. Затвор пистолета массой т 2=200 г прижимается к стволу пружиной, жесткость которой k =25 кН/м. На какое расстояние отойдет затвор после выстрела? Считать, что пистолет жестко закреплен.
23. Пружина жесткостью k =500 Н/м сжата силой F =100 Н. Определить работу А внешней силы, дополнительно сжимающей эту пружину еще на ∆ l =2 см.
24. Две пружины жесткостью k 1=0,5 кН/м и k 2=1 кН/м скреплены параллельно. Определить потенциальную энергию П данной системы при абсолютной деформации ∆ l =4 см.
25. Какую нужно совершить работу А, чтобы пружину жесткостью k =800 Н/м, сжатую на х =6 см, дополнительно сжать на ∆ х =8 см?
26. Если на верхний конец вертикально расположенной спиральной пружины положить груз, то пружина сожмется на ∆ l =3 мм. На сколько сожмет пружину тот же груз, упавший на конец пружины с высоты h =8 см?
27. Из пружинного пистолета с пружиной жесткостью k =150 Н/м был произведен выстрел пулей массой т =8 г. Определить скорость о пули при вылете ее из пистолета, если пружина была сжата на ∆ х =4 см.
28. Налетев на пружинный буфер, вагон массой т =16 т, двигавшийся со скоростью υ=0,6 м/с, остановился, сжав пружину на ∆ l =8 см. Найти общую жесткость k пружин буфера.
29. Цилиндр, расположенный горизонтально, может вращаться вокруг оси, совпадающей с осью цилиндра. Масса цилиндра т 1=12 кг. На цилиндр намотали шнур, к которому привязали гирю массой т 2=1 кг. С каким ускорением будет опускаться гиря? Какова сила натяжения шнура во время движения гири?
30. Через блок, выполненный в виде колеса, перекинута нить, к концам которых привязаны грузы массами т 1=100 г и т 2=300 г. Массу колеса М =200 г считать равномерно распределенной по ободу, массой спиц пренебречь. Определить ускорение, с которым будут двигаться грузы, и силы натяжения нити по обе стороны блока?
31. Определить скорость поступательного движения сплошного цилиндра, скатившегося с наклонной плоскости высотой h =20 см.
32. Тонкостенный цилиндр, масса которого т =12 кг, а диаметр основания D=30 см, вращается согласно уравнению 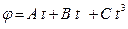 , где А =4 рад; В =-2 рад/с; С =0,2 рад/с3. Определить действующий на цилиндр момент сил М в момент времени t =3 с.
, где А =4 рад; В =-2 рад/с; С =0,2 рад/с3. Определить действующий на цилиндр момент сил М в момент времени t =3 с.
33. На обод маховика диаметром D=60 см намотан шнур, к концу которого привязан груз массой т =2 кг. Определить момент инерции J маховика, если он, вращаясь равноускоренно под действием силы тяжести груза, за время t =3 с приобрел угловую скорость ω =9 рад/с.
34. Нить с привязанными к ее концам грузами массой т 1=50 г и т 2=60 г перекинута через блок диаметром D=4 см. Определить момент инерции J блока, если под действием силы тяжести грузов он получил угловое ускорение ε=1,5 рад/с2.
35. Стержень вращается вокруг оси, проходящей через его середину согласно уравнению φ=Аt+Вt3, где А =2 рад/с; В =0,2 рад/с3. Определить вращающий момент М, действующий на стержень через t =2 с после начала вращения, если момент инерции стержня J =0,048 кгּ м2.
36. По горизонтальной плоской поверхности катится диск со скоростью υ=8 м/с. Определить коэффициент сопротивления, если диск, будучи предоставленным самому себе, остановился, пройдя путь s =18 м.
37. Определить момент силы М, который необходимо приложить к блоку, вращающемуся с частотой п =12 с-1, чтобы он остановился в течение времени ∆ t =8 с. Диаметр блока D=30 см. Массу блока т =6 кг считать равномерно распределенной по ободу.
38. Блок, имеющий форму диска массой т =0,4 кг, вращается под действием силы натяжения нити, к концам которой подвешены грузы массами т 1=0,3 кг и т 2=0,7 кг. Определить силы Т1 и Т 2 натяжения нити по обе стороны блока.
39. Шарик массой т =60 г, привязанный к концу нити длиной 1 1 =1,2 м, вращается с частотой п1 =2 с-1, опираясь на горизонтальную плоскость. Нить укорачивается, приближая шарик к оси вращения до расстояния 1 2=0,6 м. С какой частотой п 2 будет при этом вращаться шарик? Какую работу А совершает внешняя сила, укорачивая нить? Трением шарика о плоскость пренебречь.
40. По касательной к шкиву маховика в виде диска диаметром D=75 см и массой т =40 кг приложен сила F =1 кН. Определить угловое ускорение ε и частоту вращения п маховика через время t =10 с после начала действия силы, если радиус r шкива равен 12 см. Силой трения пренебречь.
41. Определить возвращающую силу F в момент времени t =0,2 с и полную энергию Е точки массой т =20 г, совершающей гармонические колебания согласно уравнению х=Аsin ωt, где A =15 см; ω =4π c-1.
42. Определить период Т колебаний стержня длиной 1 =30 см около горизонтальной оси, перпендикулярной стержню и проходящей через его конец.
43. Определить максимальное ускорение аmax материальной точки, совершающей гармонические колебания с амплитудой А =15 см, если наибольшая скорость точки υ=30 см/с. Написать также уравнение колебаний.
44. Точка совершает гармонические колебания, уравнение которых
х=Аsin ωt, где А =5 см; ω =2 c-1. В момент времени, когда точка обладала потенциальной энергией П =0,1 мДж, на нее действовала возвращающая сила F =+5 мН. Найти этот момент времени t и соответствующую ему фазу φ колебаний.
45. Определить частоту ν гармонических колебаний диска радиусом R =20 см около горизонтальной оси, проходящей через середину радиуса диска перпендикулярно его плоскости.
46. Определить период Т гармонических колебаний диска радиусом R =40 см около горизонтальной оси, проходящей через образующую диска.
47. На стержне длиной 1 =30 см укреплены два одинаковых грузика: один – в середине стержня, другой – на одном из его концов. Стержень с грузиками колеблется около горизонтальной оси, проходящей через свободный конец стержня. Определить приведенную длину L и период Т гармонических колебаний. Массой стержня пренебречь.
48. Найти максимальную кинетическую энергию Т max материальной точки массой т =2 г, совершающей гармонические колебания с амплитудой А = 4 см и частотой ν=5 Гц;
49. Точка совершает гармонические колебания. В некоторый момент времени смещение точки х =5 см, скорость ее υ=20 см/с и ускорение а =-80 см/с2. Найти циклическую частоту и период колебаний, фазу колебаний в рассматриваемый момент времени и амплитуду колебаний.
50.Точка совершает гармонические колебания, уравнение которой имеет вид 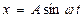 , где А=5 см; ω=2 с-1. Найти момент времени (ближайший к началу отсчета), в который потенциальная энергия точки П =10-4 Дж, а возвращающая сила F =+5·10-3 Н. Определить также фазу колебаний в этот момент времени.
, где А=5 см; ω=2 с-1. Найти момент времени (ближайший к началу отсчета), в который потенциальная энергия точки П =10-4 Дж, а возвращающая сила F =+5·10-3 Н. Определить также фазу колебаний в этот момент времени.
51. Баллон объемом V=20 л заполнен азотом при температуре T=400 К. Когда часть газа израсходовали, давление в баллоне понизилось на Δ р=200 кПа. Определить массу т израсходованного азота. Процесс считать изотермическим.
52. В баллоне объемом V= 15 л находится аргон под давлением р1=600 кПа и температуре Т1=300 К. Когда из баллона было взято некоторое количество газа, давление в баллоне понизилось до р2=400 кПа, а температура установилась Т2=260 К. Определить массу т аргона, взятого из баллона,
53. Количество вещества ν кислорода равно 0,5 моль. Определить внутреннюю энергию U водорода, а также среднюю кинетическую энергию 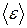 молекулы этого газа при температуре Т=З00 К.
молекулы этого газа при температуре Т=З00 К.
54. Один баллон объемом V1=10 л содержит кислород под давлением р1= 1,5 МПа, другой баллон объемом V2=22 л содержит азот под давлением р2=0,6 МПа. Когда баллоны соединили между собой, оба газа смешались, образовав однородную смесь (без изменения температуры). Найти парциальные давления р1 и р2 обоих газов в смеси и полное давление р смеси.
55. Смесь водорода и азота общей массой т =290 г при температуре Т=600 К и давлении р=2,46 МПа занимает объем V=30 л. Определить массу т 1 водорода и массу т 2 азота.
56. В баллоне объемом V=22,4 л находится водород при нормальных условиях. После того как в баллон было дополнительно введено некоторое количество гелия, давление в баллоне возросло до р=0,25 МПа, а температура не изменилась. Определить массу т гелия, введенного в баллон.
57. Водород находится при температуре Т=300 К. Найти среднюю кинетическую энергию 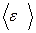 вращательного движения одной молекулы, а также суммарную кинетическую энергию Ек, всех молекул этого газа; количество вещества водорода ν=0,5 моль.
вращательного движения одной молекулы, а также суммарную кинетическую энергию Ек, всех молекул этого газа; количество вещества водорода ν=0,5 моль.
58. В азоте взвешены мельчайшие пылинки, которые движутся так, как если бы они были очень крупными молекулами. Масса т каждой пылинки равна 6∙ 10-10 г. Газ находится при температуре Т=400 К. Определить средние квадратичные скорости (υкв), а также средние кинетические энергии <εпост > поступательного движения молекулы азота и пылинки.
59. Определить показатель адиабаты у идеального газа, который при температуре Т= 350 К и давлении р= 0,4 МПа занимает объем V=300 л и имеет теплоемкость С v =857 Дж/К.
60. В сосуде объемом V=6 л находится при нормальных условиях двухатомный газ. Определить теплоемкость С v этого газа при постоянном объеме.
61. Найти среднее число (z) столкновений за время t=1 с и длину свободного пробега (1) молекулы гелия, если газ находится под давлением р =2 кПа при температуре Т =200 К.
62. Найти среднюю длину свободного пробега (1) молекулы азота в сосуде объемом V=5 л. Масса газа т =0,5 г.
63. Водород находится под давлением р =20 мкПа и имеет температуру Т =300 К. Определять среднюю длину свободного пробега (1) молекулы такого газа.
64. При нормальных условиях длина свободного пробега <1> молекулы водорода равна 0,160 мкм. Определить диаметр d молекулы водорода.
65. Какова средняя арифметическая скорость (υ) молекул кислорода при нормальных условиях, если известно, что средняя длина свободного пробега (1) молекулы кислорода при этих условиях равна 100 нм.
66. Кислород находится под давлением р=133 нПа при температуре Т =200 К. Вычислить среднее число <z> столкновений молекулы кислорода при этих условиях за время t=1 с.
67. Водород массой т =2 г занимает объем V =2,5 л. Определить среднее число (z) столкновений молекулы водорода за время τ=1 с.
68. Средняя длина свободного пробега (1) молекулы водорода при некоторых условиях равна 2 мм. Найти плотность q водорода при этих условиях.
69. При адиабатном сжатии давление воздуха было увеличено от р1=50 кПа до р2=0,5 МПа. Затем при неизменном объеме температура воздуха была понижена до первоначальной. Определить давление р3 газа в конце процесса.
70. Кислород массой т =200 г занимает объем V 1=100 л и находится.под давлением р1=200 кПа. При нагревании газ расширился при постоянном давлении до объема V 2=300 л, а затем его давление возросло до р2=500 кПа при неизменном объеме. Найти изменение внутренней энергии ∆U газа, совершенную им работу А и теплоту Q, переданную газу. Построить график процесса.
71. Объем водорода при изотермическом расширении (Т=300 К) увеличился в п =3 раза. Определить работу А, совершенную газом, и теплоту Q, полученную им при этом. Масса т водорода равна 200 г.
72. Водород массой т =40 г, имевший температуру Т=300 К, адиабатно расширился, увеличив объем в п 1=3 раза. Затем при изотермическом сжатии объем газа уменьшился в п2 =2 раза. Определить полную работу А, совершенную газом, и конечную температуру Т газа.
73. Азот массой т =0,1 кг был изобарно нагрет от температуры Т1 =200 К до температуры Т 2=400 К. Определить работу А, совершенную газом, полученную им теплоту Q и изменение ∆U внутренней энергии азота.
74. Кислород массой т =250 г, имевший температуру Т 1=200 К, был адиабатно сжат. При этом была совершена работа А =25 кДж. Определить конечную температуру Т газа.
75. Во сколько раз увеличится объем водорода, содержащий количество вещества ν=0,4 моль при изотермическом расширении, если при этом газ получит теплоту Q=800 Дж? Температура водорода Т= 300 К.
76. В баллоне при температуре Т 1=145 К и давлении р1=2 МПа находится кислород. Определить температуру Т2 и давление р2 кислорода после того, как из баллона будет очень быстро выпущена половина газа.
77. Определить работу А2 изотермического сжатия газа, совершающего цикл Карно, к. п. д. которого η=0,4, если работа изотермического расширения равна А1=8 Дж.
78. Газ, совершающий цикл Карно, отдал теплоприемнику теплоту Q2=14 кДж. Определить температуру Т1 теплоотдатчика, если при температуре теплоприемника Т2=280 К работа цикла А=6 кДж.
79. Газ, являясь рабочим веществом в цикле Карно, получил от теплоотдатчика теплоту Q1=4,38 кДж и совершил работу А=2,4 кДж. Определить температуру теплоотдатчика, если температура теплоприемника Т2=273 К.
80. Газ, совершающий цикл Карно, получает теплоту Q1=84 кДж. Определить работу 4 газа, если температура Т1 теплоотдатчика в три раза выше температуры Т2 теплоприемника.
81. Точечные заряды Q = 20 мкКл, Q=-10 мкКл находятся на расстоянии d = 5 см друг от друга. Определить напряженность поля в точке, удаленной на r1=3 см от первого и на г2 = 4 см от второго заряда. Определить также силу F, действующую в этой точке на точечный заряд Q= 1 мкК.
82. Три одинаковых точечных заряда Q1 = Q2 = Q3 = 2 нКл находятся в вершинах равностороннего треугольника со сторонами а=10см. Определить модуль и направление силы F, действующей на один из зарядов со стороны двух других.
83. Четыре одинаковых заряда Q1 = Q2 = Q3 = Q4=40 нКл закреплены в вершинах квадрата со стороной а=10 см. Найти силу F, действующую на один из этих зарядов со стороны трех остальных.
84. Точечные заряды Q1=30 мкКл и Q2= - 20 мкКл находятся на расстоянии d = 20 см друг от друга. Определить напряженность электрического поля Е в точке, удаленной от первого заряда на расстояние r1 = 30 см, а от второго — на г2= 15 см.
85. В вершинах правильного треугольника со стороной, а = 10 см находятся заряды Q1 = 10 мкКл, Q2 = 20 мкКл и Q3 = 30 мкКл. Определить силу F, действующую на заряд Q1 со стороны двух других зарядов.
86. На расстоянии d= 20 см находятся два точечных заряда Q1 = — 50 нКл и Q2=100 нКл. Определить сии F, действующую на заряд Q3= -10 нКл, удаленный от обоих зарядов на одинаковое расстояние, равное d.
87. Два точечных заряда Q1 = 6 нКл и Q2 = 3 нКл находятся на расстоянии d=60 см друг от друга. Какую работу необходимо совершить внешним силам, чтобы уменьшить расстояние между зарядами вдвое?
88. Пылинка массой m = 200 мкг, несущая на себе заряд Q = 40 нКл, влетела в электрическое поле в направлении силовых линий. После прохождения разности потенциалов U = 200 В пылинка имела скорость v = 10 м/с. Определить скорость v пылинки до того, как она влетела в поле.
89. Электрон, обладавший кинетической энергией Т = 10 Эв, влетел в однородное электрическое поле в направлении силовых линий поля. Какой скоростью будет обладать электрон, пройдя в этом поле разность потенциалов U= 8 в?
90. Пылинка массой т = 5 нг, несущая на себе N = 10 электронов, прошла в вакууме ускоряющую разность потенциалов U= 1 МВ. Какова кинетическая энергия Т пылинки? Какую скорость v приобрела пылинка?
91. Конденсаторы емкостью С1 = 5 мкФ и С2 = = 10 мкФ заряжены до напряжений U1= 60 В и U2 = = 100 В соответственно. Определить напряжение на обкладках конденсаторов после их соединения обкладками, имеющими одноименные заряды.
92. Конденсатор емкостью C1= 10 мкФ заряжен до напряжения U = 10 В. Определить заряд на обкладках этого конденсатора после того, как параллельно ему был подключен другой, незаряженный, конденсатор емкостью C1 = 20 мкФ.
93. Конденсаторы емкостями C1 = 2мкФ, C2 = = 5 мкФ и Сз = 10 мкФ соединены последовательно и находятся под напряжением U = 850 В. Определить напряжение и заряд на каждом из конденсаторов.
94. Два конденсатора емкостями С1 = 2 мкФ и С2= = 5 мкФ заряжены до напряжений U1 = 100 В и U2 = 150 В соответственно. Определить напряжение на обкладках конденсаторов после их соединения обкладками, имеющими разноименные заряды.
95. Два одинаковых плоских воздушных конденсатои емкостью С=100 Пф каждый соединены в батарею последовательно. Определить, на сколько изменится емкость С батареи, если пространство между пластинами одного из конденсаторов заполнить парафином.
96. Два конденсатора емкостями С1= 5 мкФ и С2 = 8 мкФ соединены последовательно и присоединены к батарее с ЭДС E =80 В. Определить заряды Q1 и Q2 конденсаторов и разности потенциалов U1и U2между их обкладками.
97. Плоский конденсатор состоит из двух круглых пластин радиусом R = 10 см каждая. Расстояние между пластинами d= 2 мм. Конденсатор присоединен к источика напряжения U= 80 В. Определить заряд Q и напряженность Е поля конденсатора в двух случаях: а) диэлектрик — воздух; б) диэлектрик — стекло.
98. Два металлических шарика радиусами R1 = 5 см и R2 = 10 см имеют заряды Q1 = 40 нКл и Q2 =-20 нКл соответственно. Найти энергию W, которая выделится при разряде, если шары соединить проводником.
99. Пространство между пластинами плоского конденсатора заполнено двумя слоями диэлектрика: стекла толщиной d1= 0,2 см и слоем парафина толщиной d2 = 0,3 см. Разность потенциалов между обкладками U =300 В. Определить напряженность Е поля и падение потенциала в каждом из слоев.
100. Плоский конденсатор с площадью пластин S = 200 см2 каждая заряжен до разности потенциалов U = 2 Кв. Расстояние между пластинами d = 1см. Диэлектрик — стекло. Определить энергию W поля конденсатора и плотность энергии w поля.
101. Катушка и амперметр соединены последовательно и подключены к источнику тока. К клеммам катушки присоединен вольтметр с сопротивлением г = 4 кОм. Амперметр показывает силу тока I = 0,3 А, вольтметр — напряжение U = 120 В. Определить сопротивление Rкатушки.
102. ЭДС батареи ε = 80 В, внутреннее сопротивление Ri = 5 Ом. Внешняя цепь потребляет мощность Р = 100 Вт. Определить силу тока I в цепи, напряжение U, под которым находится внешняя цепь, и ее сопротивление R.
103. От батареи, ЭДС которой 600 В, требуется передать энергию на расстояние L = 1 км. Потребляемая мощность Р = 5 кВт. Найти минимальные потери мощности в сети, если диаметр медных подводящих проводов d = 0,5 см.
104. При внешнем сопротивлении R1 = 8 Ом сила тока в цепи I1 = 0,8 А, при сопротивлении R2 = 15 Ом сила тока I2 = 0,5 А, Определить силу тока Iк.3 короткого замыкания источника ЭДС.
105. ЭДС батареи ε = 24 В. Наибольшая сила тока, которую может дать батарея, Imax= 10 А. Определить максимальную мощность Рmах, которая может выделяться во внешней цепи.
106. Аккумулятор с ЭДС ε= 12 В заряжается от сети постоянного тока с напряжением U=15 В. Определить напряжение на клеммах аккумулятора, если его внутреннее сопротивление Ri= 10 Ом.
107. От источника с напряжением U= 800 В необходимо передать потребителю мощность Р= 10 кВт на некоторое расстояние. Какое наибольшее сопротивление может иметь линия передачи, чтобы потери энергии в ней не превышали 10% от передаваемой мощности?
108. При включении электромотора в сеть с напряжением U = 220 В он потребляет ток I = 5 А. Определить мощность, потребляемую мотором, и его КПД, если сопротивление R обмотки мотора равно 6 Ом.
109. В сеть с напряжением U = 100 В подключили катушку с сопротивлением R1 = 2 кОм и вольтметр, соединенные последовательно. Показание вольтметра U1 = 80 В. Когда катушку заменили другой, вольтметр показал U2 = 60 В. Определить сопротивление R2 другой катушки.
110. ЭДС батареи ε=12 В. При силе тока I = 4 А КПД баратери η= 0,6. Определить внутреннее сопротивление Ri батареи.
111. За время t=20 с при равномерно возраставшей силе тока от нуля до некоторого максимума в проводнике сопротивлением R = 5 Ом выделилось количество теплоты Q = 4 кДж. Определить скорость нарастания силы тока.
112. Сила тока в проводнике изменяется со временем по закону I = I0e-αt, где I0 = 20 А, а α = 102с-1. Определить количество теплоты, выделившееся в проводнике за время t = 10-2 с.
113. Сила тока в проводнике сопротивлением R = 10 Ом за время t = 50 с равномерно нарастает от I1 = 5 А до I2 = 10 А. Определить количество теплоты Q, выделившееся за это время в проводнике.
114. В проводнике за время t= 10 с при равномерном возрастании силы тока от I1 = 1 А до I2 = 2 А выделилось количество теплоты Q = 5 кДж. Найти сопротивление Rпроводника.
115. Сила тока в проводнике изменяется со временем по закону I = Iоsinωt Найти заряд Q, проходящий через поперечное сечение проводника за время t, равное половине периода T, если начальная сила тока I0 = 10 А, циклическая частота ω = 50πс-1.
116. За время t = 10 с при равномерно возрастающей силе тока от нуля до некоторого максимума в проводнике выделилось количество теплоты Q = 40 кДж. Определить среднюю силу тока <I> в проводнике, если его сопротивление R = 25 Ом.
117. За время t=8 с при равномерно возраставшей силе тока в проводнике сопротивлением R = 8 Ом выделилось количество теплоты Q = 500 Дж. Определить заряд q, проходящий в проводнике, если сила тока в начальный момент времени равна нулю.
118. Определить количество теплоты Q, выделившееся за время t = 10 с в проводнике сопротивлением R = 10 Ом, если сила тока в нем, равномерно уменьшаясь, изменилась от I1 = 10 А до I2 = 0.
119. Сила тока в цепи изменяется по закону I = Iоsinωt. Определить количество теплоты, которое выделится в проводнике сопротивлением R=10 Ом за время, равное четверти периода (от t1 = 0 до t2 = Т/4, где Т=10 с).
120. Сила тока в цепи изменяется со временем по закону I = Iое-αt. Определить количество теплоты, которое выделится в проводнике сопротивлением R = 20 Ом за время, в течение которого ток уменьшится в е раз. Коэффициент α = 2ּ10-2с -1.
121. Определить индукцию магнитного поля двух длинных прямых параллельных проводников с одинаково направленными токами I1 = 0,2 А и I2 = 0,4 А в точке, лежащей на продолжении прямой, соединяющей проводники с токами, на расстоянии r = 2 см от второго проводника. Расстояние между проводниками l = 10 см.
122. Два длинных прямых параллельных проводника, по которым текут в противоположных направлениях токи I1 = 0,2 А и I2 = 0,4 А, находятся на расстоянии l = 14 см. Найти индукцию магнитного поля в точке, расположенной между проводниками на расстоянии r = 4 см от первого из них.
123. По двум длинным прямым параллельным проводникам в одном направлении текут токи I1 = 1 А и I2 = 3 А. Расстояние между проводниками r = 40 см. Найти индукцию магнитного поля в точке, находящейся посередине между проводниками.
124. Определить напряженность и индукцию магнитного поля у стенки длинной электронно-лучевой трубки диаметром d = 6 см, если через сечение электронного шнура проходит 1018 электронов в 1 с. Считать электронный шнур тонким и центральным.
125. Два параллельных длинных проводника с токами I = 2 А, текущими в противоположных направлениях, расположены на расстоянии r = 15 см друг от друга. Определить индукцию магнитного поля в точке, лежащей между проводниками, на расстоянии r1 = 3 см от второго проводника.
126. По двум длинным прямым и параллельным проводникам текут в одном направлении токи I1 = 2 А и I2 = 3 А. Расстояние между проводниками r = 12 Ом. Найти индукцию магнитного поля в точке, лежащей на отрезке прямой, соединяющей проводники, на расстоянии r1 = 2 см от первого проводника.
127. Два длинных прямых параллельных проводника, по которым текут в противоположных направлениях токи I1 = 0,2 А и I2 = 0,4 А, расположены на расстоянии r = 12 см друг от друга. Определить индукцию магнитного поля в точке, лежащей в середине отрезка прямой, соединяющего проводники.
128. Определить индукцию магнитного поля двух длинных прямых параллельных проводников с одинаково направленными токами I = 10 А в точке, расположенной на продолжении прямой, соединяющей проводники с токами, на расстоянии а = 10 см от второго провода. Расстояние между проводниками r = 40 см.
129. По двум длинным проводникам, расположенным параллельно на расстоянии r = 15 см друг от друга, текут в противоположных направлениях токи I1 = 10 А и I2 = 5 А. Определить индукцию магнитного поля в точке, расположенной на расстоянии r1 = 5 см от первого проводника, на продолжении отрезка прямой, соединяющего проводники.
130. Индукция В магнитного поля в центре проволочного кольца радиусом r = 20 см, по которому течет ток, равна 4 мкТл. Найти разность потенциалов на концах кольца, если его сопротивление R = 3,14 Ом.
131. Два иона разных масс с одинаковыми зарядами влетели в однородное магнитное поле, стали двигаться по окружностям радиусами R1 = 3см и R2=1,73см. Определить отношение масс ионов, если они прошли одинаковую ускоряющую разность потенциалов.
132. Однозарядный ион натрия прошел ускоряющую разность потенциалов U=1Кв и влетел перпендикулярно линиям магнитной индукции в однородное поле (В = 0,5Тл). Определить относительную атомную массу А иона, если он описал окружность радиусом R = 4,37 см.
133. Электрон прошел ускоряющую разность потенциалов U = 800 В и, влетев в однородное магнитное поле В = 47 мТл, стал двигаться по винтовой линии с шагом h = 6 см. Определить радиус R винтовой линии.
134. Альфа-частица прошла ускоряющую разность потенциалов U=300 В и, попав в однородное магнитное поле, стала двигаться по винтовой линии радиусом R=1 см и шагом h = 4см. Определить магнитную индукцию В поля.
135. Заряженная частица прошла ускоряющую разность потенциалов U= 100 В и, влетев в однородное магнитное поле (В = 0,1 Тл), стала двигаться по винтовой линии с шагом h = 6,5 см и радиусом R=1 см. Определить отношение заряда частицы к ее массе.
136. Электрон влетел в однородное магнитное поле (В=200мТл) перпендикулярно линиям магнитной индукции. Определить силу эквивалентного кругового тока Iэкв, создаваемого движением электрона в магнитном поле.
137. Протон прошел ускоряющую разность потенциалов U=300 В и влетел в однородное магнитное поле (В = 20мТл) под углом a=30° к линиям магнитной индукции. Определить шаг h и радиус R винтовой линии, по которой будет двигаться протон в магнитном поле.
138. Альфа-частица, пройдя ускоряющую разность потенциалов U, стала двигаться в однородном магнитном поле (В = 50мТл) по винтовой линии с шагом h = 5 см и радиусом R= 1 см. Определить ускоряющую разность потенциалов, которую прошла альфа-частица.
139. Ион с кинетической энергией Т= 1 кэВ попал в однородное магнитное поле (B = 21 мТл) и стал двигаться по окружности. Определить магнитный момент рт эквивалентного кругового тока.
140. Ион, попав в магнитное поле (В = 0,01 Тл), стал двигаться по окружности. Определить кинетическую энергию Т (в Эв) иона, если магнитный момент рт эквивалентного кругового тока равен 1,6×1014 А×м2.
141. Плоский контур площадью S = 20 см2 находится в однородном магнитном поле (B = 0,03 Тл). Определить магнитный поток Ф, пронизывающий контур, если плоскость его составляет угол φ = 60◦ с направлением линий индукций.
142. Магнитный поток Ф сквозь сечение соленоида 50мкВб. Длина соленоида l=50 см. Найти магнитный момент рm соленоида, если его витки плотно прилегают друг к другу.
143. В средней части соленоида, содержащего п = 8 витков/см, помещен круговой виток диаметром d = 4 см. Плоскость витка расположена под углом φ = 60° к оси соленоида. Определить магнитный поток Ф, пронизывающий виток, если по обмотке соленоида течет ток I=1 А.
144. На длинный картонный каркас диаметром d= 5 см уложена однослойная обмотка (виток к витку) из проволоки диаметром d=0,2 мм. Определить магнитный поток Ф, создаваемый таким соленоидом при силе тока I=0,5 А.
145. Квадратный контур с стороной а=10см, в котором течет ток I=6А, находится в магнитном поле (В = 0,8 Тл) под углам a=50° к линиям индукции. Какую работу А нужно совершить, чтобы при неизменной силе тока в контуре изменить его форму на окружность?
146. Плоский контур с током I=5 А свободно установился в однородном магнитном поле (В = 0,4 Тл). Площадь контура S= 200 см2. Поддерживая ток в контуре неизменным, его повернули относительно оси, лежащей в плоскости контура, на угол a= 40°. Определить совершенную при этом работу А.
147. Виток, в котором поддерживается постоянная сила тока I=60 А, свободно установился в однородном магнитном поле (В = 20 мТл). Диаметр витка d = 10 см. Какую работу А нужно совершить для того, чтобы повернуть виток относительно оси, совпадающей с диаметром, на угол a= π/3?
148. В однородном магнитном поле перпендикулярно линиям индукции расположен плоский контур площадью S=100 см2. Поддерживая в контуре постоянную силу тока I=50 А, его переместили из поля в область пространства, где поле отсутствует. Определить магнитную индукцию В поля, если при перемещении контура была совершена работа А = 0,4 Дж.
149. Плоский контур с током I=50 А расположен в однородном магнитном поле (B= 0,6 Тл) так, что нормаль к контуру перпендикулярна линиям магнитной индукции. Определить работу, совершаемую силами поля при медленном повороте контура около оси, лежащей в плоскости контура, на угол a=30°.
150. Определить магнитный поток Ф, пронизывающий соленоид, если его длина l=50 см и магнитный момент рm= 0,4 Bб.
151. Соленоид сечением S= 10 см2 содержит N = 10 3 витков. При силе тока I=5А магнитная индукция В поля внутри соленоида равна 0,05 Тл. Определить индуктивность Lсоленоида.
152. На картонный каркас длиной l=0,8м и диаметром D = 4 см намотан в один слой провод диаметром d= 0,25 мм так, что витки плотно прилегают друг к другу. Вычислить индуктивность I получившегося соленоида.
153. Катушка, намотанная на магнитный цилиндрический каркас, имеет N=250 витков и индуктивность L1= 36 мГн. Чтобы, увеличить индуктивность катушки до L2 =100 мГн, обмотку катушки сняли и заменили обмоткой из более тонкой проволоки с таким расчетом, чтобы длина катушки осталась прежней. Сколько витков оказалось в катушке после перемотки?
154. Индуктивность Lсоленоида, намотанного в один слой на немагнитный каркас, равна 0,5 мГн. Длина l соленоида равна 0,6м, диаметр D = 2 см. Определить отношение п числа витков соленоида к его длине.
155. Соленоид содержит H = 800 витков. Сечение сердечника (из немагнитного материала) S =10 см2. По обмотке течет ток, создающий поле с индукцией В=8 мТл. Определить среднее значение ЭДС < e s> самоиндукции, которая возникает на зажимах соленоида, если сила в тока уменьшается практически до нуля за время ∆t = 0,8 мс.
156. По катушке индуктивностью L = 8 мкГн течет ток I = 6 А. Определить среднее значение ЭДС < e s > самоиндукции, возникающей в контуре, если сила тока изменится практически до нуля за время ∆t = 5 мс.
157. В электрической цепи, содержащей резистор сопротивлением R = 20 Ом и катушку индуктивностью L= 0,06 Гн, течет ток I=20 А. Определить силу тока I в цепи через ∆t=0,2 мс после ее размыкания.
158. Цепь состоит из катушки индуктивностью L =0,1 Гн и источника тока. Источник тока отключили, не разрывая цепи. Время, через которое сила тока уменьшится до 0,001 первоначального значения, равно t=0,07 с. Определить сопротивление катушки.
159. Источник тока замкнули на катушку сопротивлением R=10 Ом и индуктивностью L = 0,2 Гн. Через какое время сила тока в цепи достигнет 50 % максимального значения?
160. Источник тока замкнули на катушку сопротивлением R = 20 Ом. Через время t = 0,1 с тока I в катушке достигла 0,95 предельного значения. Определить индуктивность Lкатушки.
161. Между стеклянной пластинкой и лежащей на ней плосковыпуклой линзой находиться жидкость. Найти показатель преломления жидкости, если радиус r3 третьего темного кольца Ньютона при наблюдении в отраженном свете с длиной волны λ =0,6 мкм равен 0,82 мм. Радиус кривизны линзы R=0,5 м.
162. На тонкую пленку в направлении нормали к ее поверхности падает монохроматический свет с длиной волны λ=500 нм. Отраженный от нее свет максимально усилен вследствие интерференции. Определить минимальную толщину dmin пленки, если показатель преломления материала пленки n=1,4.
163. Расстояние L от щелей до экрана в опыте Юнга равно 1 м. Определить расстояние между щелями, если на отрезке длиной l=1 см укладывается N=10 темных интерференционных полос. Длина волны λ=0,7 мкм.
164. На стеклянную пластину положена выпуклой стороной плосковыпуклая линза. Сверху линза освещена светом длиной волны λ=500 нм. Найти радиус R линзы, если радиус четвертого, темного кольца Ньютона в отраженном свете r4=2 мм.
165. На тонкую глицериновую пленку толщиной d=1,5 мкм нормально к ее поверхности падает белый свет. Определить длины волн λ лучей видимого участка спектра (0,4 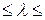 0,8 мкм), которые будут ослаблены в результате интерференции.
0,8 мкм), которые будут ослаблены в результате интерференции.
166. На стеклянную пластину нанесен тонкий слой прозрачного вещества с показателем преломления n=1,3. Пластинка освещена параллельным пучком монохроматического света с длиной волны λ=640 нм, падающим на пластинку нормально. Какую минимальную толщину dmin должен иметь слой, чтобы отраженный пучок имел наименьшую яркость?
167. На тонкий стеклянный клин падает нормально параллельный пучок света с длиной волны λ = 500 нм. Расстояние между соседними темными интерференционными полосами в отраженном свете b = 0,5 мм. Определить угол α между поверхностями клина. Показатель преломления стекла, из которого изготовлен клин n=1,6.
168. Плосковыпуклая стеклянная линза с f = 1 м лежит выпуклой стороной на стеклянной пластинке. Радиус пятого темного кольца Ньютона в отраженном свете r5= 1,1 мм. Определить длину световой волны λ ..
169. Между двумя плоскопараллельными пластинами на расстоянии L = 10 см от границы их соприкосновения находится проволока диаметром d = 0,01 мм, образуя воздушный клин. Пластины освещаются нормально падающим монохроматическим светом (λ = 0,6 мкм). Определить ширину в интерференционных полос, наблюдаемых в отраженном свете.
170. Установка для наблюдения колец Ньютона освещается нормально падающим монохроматическим светом (λ=590 нм). Радиус кривизны R линзы равен 5 см. Определить толщину d3 воздушного промежутка в том месте, где в отраженном свете наблюдается третье светлое кольцо.
171. Какое наименьшее число Nmin штрихов должна содержать дифракционная решетка, чтобы в спектре второго порядка можно было видеть раздельно две желтые линии натрия с длинами волн λ1 = 589,0 нм и λ 2= 589,6 нм? Какова длина l такой решетки, если постоянная решетки d = 5 мкм?
172. На поверхность дифракционной решетки нормально к ее поверхности падает монохроматический свет. Постоянная дифракционной решетки в п = 4,6 раза больше длины световой волны. Найти общее число М дифракционных максимумов, которые теоретически можно наблюдать в данном случае.
173. На грань кристалла каменной соли падает параллельный пучок рентгеновского излучения. Расстояние dмежду атомными плоскостями равно 280 пм. Под углом θ=6 5° к атомной плоскости наблюдается дифракционный максимум первого порядка. Определить длину волны λрентгеновского излучения.
174. На непрозрачную пластину с узкой щелью падает нормально плоская монохроматическая световая волна (λ=600 нм). Угол отклонения лучей, соответствующих второму дифракционному максимуму, φ=200. Определить ширину а щели.
175. На дифракционную решетку, содержащую n=100 штрихов на 1 мм, нормально падает монохроматический свет. Зрительная труба спектрометра наведена на максимум второго порядка. Чтобы вывести трубу на другой максимум того же порядка, ее нужно повернуть на угол Δφ=160. Определить длину волны λ света, падающего на решетку
176. На дифракционную решетку падает нормально монохроматический свет (λ=410нм). Угол Δφ между направлениями на максимумы первого и второго порядков равен 2°21'. Определить число n штрихов на 1 мм дифракционной решетки.
177. Постоянная дифракционной решетки в n=4 раза больше световой волны монохроматического света, нормально падающего на поверхность. Опреде-
лить угол α между двумя первыми симметричными ди-
фракционными максимумами..
178. Расстояние между штрихами дифракционной решетки d=4 мкм. На решетку падает нормально свет с длиной волны λ == 0,58 мкм. Максимум, какого наибольшего порядка дает эта решетка?
179. На пластину с щелью, ширина которой а= 0,05 мм, падает нормально монохроматический свет с длиной волны λ=0,7 мкм. Определить угол φ отклонения лучей, соответствующий первому дифракционному максимуму.
180.Дифракционная решетка, освещенная нормально падающим монохроматическим светом, отклоняет спектр третьего порядка на угол φ1=300. На какой угол φ2 отклоняет она спектр четвертого порядка.
181. Параллельный пучок света переходит из глицерина к стекло так, что пучок, отраженный от границе раздела этих сред, оказывается максимально поляризованным. Определить угол γ между падающим и преломленным пучком.
182. При прохождении света через трубку длиной l1=20 см., содержащую раствор сахара концентрацией =10 %, плоскость поляризации света, повернулась на угол φ1=13,30. В другом растворе сахара, налитом в трубку l2=15 см., плоскость поляризации повернулась на угол φ2=5,20. Определить концентрацию C2 второго раствора..
183. Угол падения ε луча на поверхность стекла равен 60 0. При этом отраженный пучок света оказался максимально поляризованным.. Определить угол ε2 преломления луча..
184. Пучок света переходит из жидкости в стекло. Угол падения ε пучка равен 600, угол преломления ε2=500. При каком угле падения εВ пучок света, отраженный от границы раздела этих сред, будем максимально поляризован?
185. Пучок света падает на плоскопараллельную стеклянную пластину, нижняя поверхность которой находится в воде.. При каком угле падения εВ свет, отраженный от границы стекло- вода, будет максимально поляризован?
186. Естественный свет проходит через два поляризатора, угол между главными плоскостями которых равен 30 0. Во сколько раз уменьшится интенсивность света после прохождения этой системы? Считать, что каждый поляризатор отражает и поглощает 10% падающего света.
187. Чему равен угол между главными плоскостями двух поляризаторов, если интенсивности света, прошедшего через них, уменьшилась в 5,3 раза? Считать, что каждый поляризатор отражает и поглощает 13% падающего света.
188. Естественный свет проходит через два поляризатора, угол между главными плоскостями которых равен 30 0. Во сколько раз изменится интенсивность света, прошедшего эту систему, если угол между плоскостями поляризаторов увеличить в два раза?
189. Под каким углом к горизонту должно находиться Солнце, чтобы его лучи, отраженные от поверхности воды, были максимально поляризованы?
190. Раствор сахара с концентрацией 0,25 г/см3 толщиной 18 см поворачивает плоскость поляризации монохроматического света на угол 30 0. Другой раствор толщиной 16 см поворачивает плоскость поляризации этого же света на угол 24 0. Определить концентрацию сахара во втором растворе.
191. Черное тело имеет температуру Т1 = 500 К. Какова будет температура Т2 тела, если в результате нагревания поток излучения увеличится в n = 5 раз?
192. Температура абсолютно черного тела Т=2кК. Определить длину волны λm на которую приходится максимум энергии излучения, и спектральную плотность энергетической светимости (излучательности) (r λ,T)max для этой длины волны.
193. Определить температуру Т и энергетическую светимость (нзлучательность) Rе абсолютно чертога тела, если максимум энергии излучения приходится на длину волны λ т = 600 нм.
194. Из смотрового окошечка печи излучается поток Фе = 4 кДж/мин. Определить температур Т печи, если площадь окошечка S=8 см2. >
195. Поток излучения абсолютно черного тела Фе = 10 кВт. Максимум энергии излучения приходится на длину волны λm= 0,8 мкм. Определить площадь S излучающей поверхности..
196. Как и во сколько раз изменится поток излучения абсолютно черного тела, если максимум энергии излучения переместится с красной границы видимого спектра (λm1 =780 нм) на фиолетовую (λm2= 390 им)?
197. Определить поглощательную способность aТ серого тела, для которого температура, измеренная радиационным пирометром, Трад= 1,4 кК, тогда как истинная температура Т тела равна 3,2 кК.
198. Средняя энергетическая светимость R поверхности Земли равна 0,54 Дж/(см2· мин). Какова должна быть температура Т поверхности Земли, если условно считать, что она излучает как серое тело с коэффициентом черноты аТ= 0,25?
199. Вычислить энергию, излучаемую за время t=1 мин с площади S=1 см2 абсолютно черного тела, температура которого Т=1000 К.
200. Длина волны, на которую приходиться максимум энергии излучения абсолютно черного тела, λm=0,6 мкм. Определить температуру тела.
201. Красная граница фотоэффекта для цинка λ0 = 310 нм. Определить максимальную кинетическую энергию Тmax фотоэлектронов в электрон-вольтах, если на цинк падает свет с длиной волны λ=200 нм.
202. На поверхность калия падает свет с длиной волны λ = 150 нм. Определить максимальную кинетическую энергию Тmax фотоэлектронов.
203. Фотон с энергией ε=10 эВ падает на серебряную пластину и вызывает фотоэффект. Определить импульс р, полученный пластиной, если принять, что направления движения фотона и фотоэлектрона лежат на одной прямой, перпендикулярной поверхности пластин.
204. На фотоэлемент с катодом из лития падает свет с длиной волны λ = 200 нм. Найти наименьшее значение задерживающей разности потенциалов U min, которую нужно приложить к фотоэлементу, чтобы прекратить фототок.
205. Какова должна быть длина волны γ-излучения, падающего на платиновую пластину, чтобы максимальная скорость фотоэлектронов была υmax= 3 Мм/с?
206. На металлическую пластину направлен пучок ультрафиолетового излучения (λ=0,25 мкм). Фототок прекращается при минимальной задерживающей разности потенциалов Umin= 0,96 В. Определить работу выхода А электронов из металла.
207. На поверхность металла падает монохроматический свет с длиной волны λ = 0,1 мкм. Красная граница фотоэффекта λ0 = 0,3 мкм. Какая доля энергии фотона расходуется на сообщение электрону кинетической энергии?
208. На металл падает рентгеновское излучение с длиной волны λ = 1 нм. Пренебрегая работой выхода, определить максимальную скорость υmax фотоэлектронов.
209. На металлическую пластину направлен монохроматический пучок света с частотой ν=7,3·1014 Гц. Красная граница λ0 фотоэффекта для данного материала равна 560 нм. Определить максимальную скорость υmaxфотоэлектронов.
210. На цинковую пластину направлен монохроматический пучок света. Фототок прекращается при задерживающей разности потенциалов U= 1,5 В. Определить длину волны λ света, падающего на пластину.
211. Давление р света с длиной волны λ= 40 нм, падающего нормально на черную поверхность, равно 2 нПа. Определить число N фотонов, падающих за время t=10 с на площадь S=1 мм2 этой поверхности.
212. Определить коэффициент отражения р поверхности, если при энергетической освещенности Ее= 120 Вт/ м2 давление р света на нее оказалось равным 0, 5 мк Па.
213. Давление света, производимое на зеркальную поверхность, р= 5 мПа. Определить концентрацию n0 фотонов вблизи поверхности, если длина волны света, падающего на поверхность, λ= 0,5 мкм.
214. На расстоянии г =5 мот точечного монохроматического (λ=0,5 мкм) изотропного источника расположена площадка (S = 8 мм2) перпендикулярно падающим пучкам. Определить число N фотонов, ежесекундно падающих на площадку. Мощность излучения Р =100 Вт.
215. На зеркальную поверхность под углом α = 60° к нормали падает пучок монохроматического света (λ= 590 нм), Плотность потока энергии светового пучка φ= 1 кВт/м2. Определить давление р, производимое светом на зеркальную поверхность.
216. Свет надает нормально на зеркальную поверх-
ность, находящуюся на расстоянии г=10 см от тотеч-
ного изотропного излучателя. При какой мощности Р
излучателя давление р на зеркальную поверхность будет
равным 1 мПа?
217. Свет с длиной волны λ=600 нм нормально падает на зеркальную поверхность и производит на нее давление р =4 мкПа. Определить число N фотонов, падающих за время t=10 с на площадь S=1 мм2 этой поверхности.
218. На зеркальную поверхность площадью S = 6 см2 падает нормально поток излучения Фе = 0,8 Вт. Определить давление р и силу давления F света на эту поверхность.
219. Точечной источник монохроматического (λ = 1 нм) излучения находится в центре сферической зачерненной колбы радиусом R = 10 см. Определить световое давление р, производимое на внутреннюю поверхность колбы, если мощность источника Р=кВт.
220. Поток энергии, излучаемой электрической лампой, Фе=600 Вт. На расстоянии r=1 м от лампы перпендикулярно падающим лучам расположено круглое плоское зеркальце диаметром d=2 см. Определить силу F светового давления на зеркальце. Лампу рассматривать как точечный изотропный излучатель
221. Невозбужденный атом водорода поглощает квант излучения с длиной волны λ = 102,6 нм. Вычислить, пользуясь теорией Бора, радиус rэлектронной орбиты возбужденного атома водорода.
222. Вычислить по теории Бора радиус r2второй стационарной орбиты и скорость υ2 электрона на этой орбите для атома водорода.
223. Вычислить по теории Бора период Т вращения электрона в атоме водорода, находящегося в возбужденном состоянии, определяемом главным квантовым числом n = 2.
224. Определить изменение энергии Δ E электрона в атоме водорода при излучении атомом фотона с частотой ν= 6,28ּ1014 Гц.
225. Во сколько раз изменится период Т вращения электрона в атоме водорода, если при переходе в невозбужденное состояние атом излучил фотон с длиной волны λ = 97,5нм?
226. На сколько изменилась кинетическая энергия электрона в атоме водорода при излучении атомом фотона с длиной волны λ = 435нм?
227. В каких пределах Δλ, должна лежать длина волн монохроматического света, чтобы при возбуждении атомов водорода квантами этого света радиус rn орбиты электрона увеличился в 16 раз?
228. В однозарядном ионе лития электрон перешел с четвертого энергетического уровня на второй. Определить длину волны λ излучения, испущенного ионом лития?
229. Электрон в атоме водорода находится на третьем энергетическом уровне. Определить кинетическую T, потенциальную П, полную Е энергии электрона. Ответ выразить в электрон-вольтах.
230. Фотон выбивает из атома водорода, находящегося в основном состоянии, электрон с кинетической энергией Е=10эВ.Определить энергию ε фотона.
231. Найти период полураспада T1/2 радиоактивного изотопа, если его активность за время t=10 сут уменьшилось на 24% по сравнению с первоначальной.
232.Определить,какая доля радиоактивного изотопа 
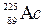 распадается в течение времени t= 6 сут.
распадается в течение времени t= 6 сут.
233. Активность А некоторого изотопа за время t= 10 сут уменьшилась на 20%. Определить период полураспада T1/2этого изотопа.
234. Определить массу m изотопа 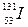 , имеющего активность А= 37 ГБк.
, имеющего активность А= 37 ГБк.
235. Найти среднюю продолжительность жизни τ атома радиоактивного изотопа кобальта 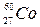 .
.
236. Счетчик α-частиц, установленный вблизи радиоактивного изотопа, при первом измерении регистрировал N1 = 1400 частиц в минуту, а через время t= 4 ч — только N2= 400. Определить период полураспада T1/2 изотопа.
237. Во сколько раз уменьшится активность изотопа 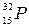 через время t=20 сут?
через время t=20 сут?
238. На сколько процентов уменьшится активность изотопа иридия 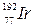 за время t= 15сут?
за время t= 15сут?
239. Определить число N ядер, распадающихся в течение времени: 1) t1= 1 мин; 2) t2 = 5 сут, — в радиоактивном изотопе фосфора 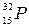 массой m= 1 мг.
массой m= 1 мг.
240. Из каждого миллиона атомов радиоактивного изотопа каждую секунду распадается 200 атомов. Определить период полураспада T1/2изотопа.
241. Вычислить энергию ядерной реакции
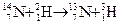 .
.
Выделяется или поглощается эта энергия?
242. Подтвердить расчетом, что при ядерной реакции
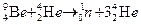
поглощается 1,56 МэВ.
243. Сколько энергии поглощается при ядерной реакции
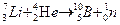
244. Сколько энергии выделяется при ядерной реакции
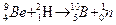 ?
?
245. Подтвердить расчетом, что при ядерной реакции
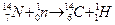
выделится 0,624 МэВ.
246. Ядро изотопа фосфора 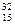 P выбросило отрицательную β-частицу. В какое ядро превратилось ядро фосфора? Написать реакцию и вычислить дефект массы нового ядра.
P выбросило отрицательную β-частицу. В какое ядро превратилось ядро фосфора? Написать реакцию и вычислить дефект массы нового ядра.
247. Подтвердить расчетом, что при ядерной реакции
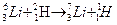
выделится энергия 5,02 МэВ.
248. Вычислить энергию термоядерной реакции
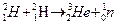
249. Вычислить энергетический эффект Q реакции
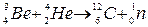
250.То же, для реакции 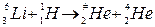
251. Вычислить дефект массы и энергию связи ядра дейтерия 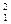 H.
H.
252. Сколько энергии освободится при соединении одного протона и двух нейтронов в атомное ядро?
253. Найти удельную энергию связи, т. е. энергию связи, приходящуюся на один нуклон ядра изотопа 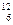 C.
C.
254. Определить дефект массы и энергию связи ядра трития 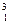 H.
H.
255. Вычислить удельную энергию связи, т. е. энергию связи, приходящуюся на один нуклон ядра 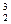 Не.
Не.
256. Сколько энергии необходимо затратить для того, чтобы ядро гелия 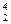 Не разделить на нуклоны?
Не разделить на нуклоны?
257. Сколько энергии выделится при образовании одного ядра 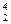 Не из протонов и нейтронов?
Не из протонов и нейтронов?
|
|
 2015-01-30
2015-01-30 1182
1182
