Плотность потока энергии волны. Вектор Умова

ЛЕКЦИЯ 10

Плотностью потока энергии волны называется вектор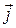, направленный в сторону распространения волны и численно равный отношению потока энергии d Φ, сквозь малый элемент dS поверхности к площади dS_n проекции этого элемента на плоскость, перпендикулярную к направлению распространения волны:

.

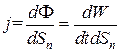Выразим плотность потока энергии через объемную плотность энергии w. Согласно определению, плотность потока энергии волны равна

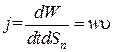, (10.1)

где энергия dW = w u dtdS_n равна энергии, переносимой через попереч-

ное сечение параллелепипеда, dS_n, перпендикулярное к направлению распространения волны. Объем данного параллелепипеда равен u dtdS_n (см. рис. 10.2).

Направление вектора плотности потока энергии 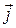совпадает с направлением скорости 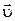распространения волны, т. е.

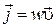. (10.2)

Таким образом, вектор плотности потока энергии волны равен произведению вектора скорости распространения энергии волны на величину ее объемной плотности. Вектор 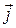называется вектором Умова.

Из формул (10.18) и (10.19) следует, что объемная плотность энергии и плотность потока энергии синусоидальной волны пропор

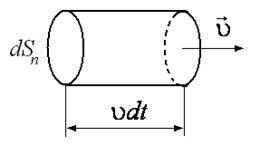
Рис. 10.1

циональны квадрату амплитуды волны и квадрату частоты волны. Формула (10.20) справедлива для плотности потока энергии волн любого типа.