Особенности расчета электромагнитных процессов в катушке с магнитопроводом и переменной МДС

Для примера возьмем П-образный электромагнит переменного тока с к.з. витком на полюсе (Рис.1).

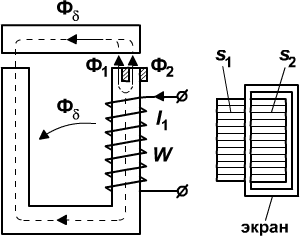
Рисунок 1

где

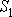	—	площадь полюса, не охваченная экраном,
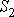	—	экранированная площадь полюса.

Магнитный поток 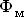, проходя в воздушный зазор разветвляется на два потока, один из которых 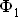проходит через неохваченную экраном часть полюса, а другой 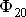про ходит через экран и наводит в нем эдс. Возникающий при этом в экране ток создает в экранированной части полюса свой магнитный поток 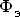, направленный встречно по отношению к потоку и замыкающийся через воздушный зазор и якорь. В результате совместного действия потоков 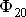и 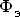результирующий поток 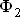в экранированной части полюса будет сдвинут по фазе на угол 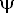относительно потока 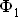в неохваченной экраном части полюса. Таким образом, в воздушном зазоре благодаря экрану действуют два магнитных потока, сдвинутых друг относительно друга по фазе. Это способствует устранению вибрации якоря электромагнита переменного тока.

Векторная диаграмма электромагнита с экраном показана на (Рис. 2)

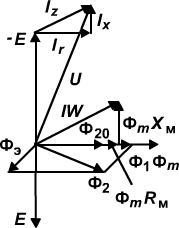
Рисунок 2

Составим схему замещения магнитной цепи с учетом влияния потерь в стали и экрана

Решаем прямую задачу. Дано: поток в воздушном зазоре, размеры магнитной цепи и материал магнитопровода (Рис. 3).Найти намагничивающую силу катушки.

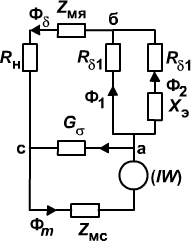
Рисунок 3

1) Известным методом определяются магнитные сопротивления (проводимости) воздушных зазоров и проводимость рассеяния

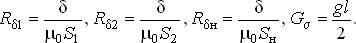(1)

2) Определяется магнитное напряжение между точками ab схемы

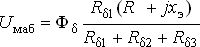(2)

здесь

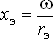	—	активное сопротивление экрана,
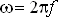	—	угловая частота сети.

3) Индукция в якоре 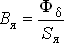, 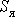— площадь сечения якоря,

4) Магнитное сопротивление якоря. По кривой намагничивания B (H) определяется напряженность магнитного поля 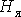и затем

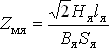(3)

Если это необходимо, то можно найти также

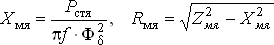(4)

Здесь

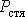	—	потери в стали якоря,
f	—	частота сети.

5) Магнитное напряжение в якоре

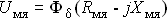(5)

6) Магнитное напряжение между точками ac

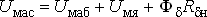(6)

7) Поток рассеяния

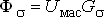(7)

8) Поток в основании электромагнита

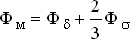(8)

9) Магнитное напряжение в сердечнике

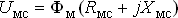(9)

10) Искомаямдс катушки

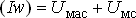(10)

При решении обратной задачи необходимо задаться потоком 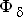и решать методом последовательных приближений.