Рассмотрим самый общий случай теплообмена излучением между двумя телами, когда одно тело заключено внутри другого (например, отопительная батарея находится внутри комнаты).
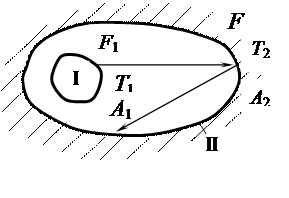 Постановка задачи. Пусть тело I расположено внутри другого тела II, которое называется оболочкой.
Постановка задачи. Пусть тело I расположено внутри другого тела II, которое называется оболочкой.
Для тела I известно: 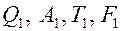 ,
, 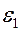 , а для второго
, а для второго
тела: 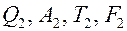 ,
, 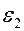 . Задача стационарная. Пусть
. Задача стационарная. Пусть 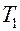 >
> 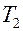 . .Необходимо определить
. .Необходимо определить 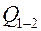 .
.
Согласно определению
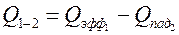 ,
,
где 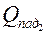 – падающее тепловое излучение со второго тела на первое. В отличие от ранее рассмотренного случая, не все лучи со второго тела достигнут первого, часть из них пройдет мимо. Поэтому
– падающее тепловое излучение со второго тела на первое. В отличие от ранее рассмотренного случая, не все лучи со второго тела достигнут первого, часть из них пройдет мимо. Поэтому
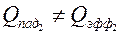 .
.
Введем некоторый коэффициент 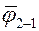 , так, чтобы
, так, чтобы
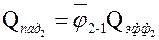 .
.
Коэффициент 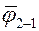 характеризует долю излучения второго тела, которое падает на первое, и называется средним угловым коэффициентом излучения. Тогда уравнение можно записать в виде
характеризует долю излучения второго тела, которое падает на первое, и называется средним угловым коэффициентом излучения. Тогда уравнение можно записать в виде
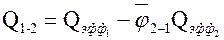 ,
,
где, согласно соотношению,
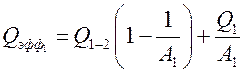 ,
,
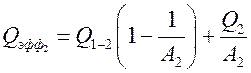 .
.
Подставляя эти выражения в расчетное уравнение и учитывая, что при стационарном режиме 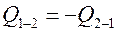 , получаем
, получаем
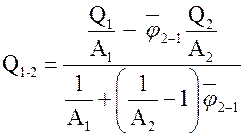 .
.
Используя закон Стефана-Больцмана и следствие из закона Кирхгофа, запишем 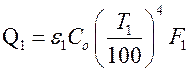 ,
, 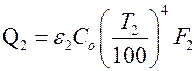 ,
,
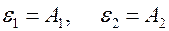 . Тогда расчетное уравнение будет иметь вид
. Тогда расчетное уравнение будет иметь вид
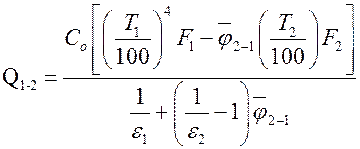 .
.
Определим средний угловой коэффициент излучения. Для этого предположим, что 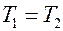 , тогда
, тогда 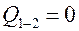 . Это возможно, если числитель формулы равен нулю. Поскольку
. Это возможно, если числитель формулы равен нулю. Поскольку 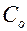 не равняется нулю, значит,
не равняется нулю, значит,
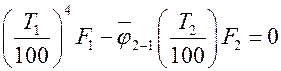 .
.
Отсюда 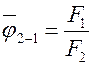 .
.
Окончательно формула для теплообмена излучением между телом и оболочкой примет вид
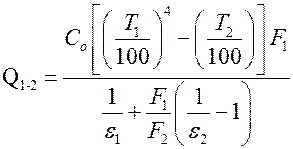 .
.
Частные случаи. Рассмотрим следующие два частных случая:
1. Если 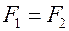 , то
, то 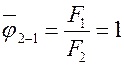 .
.
Тогда
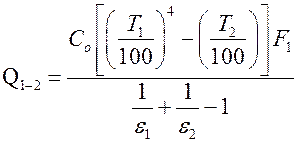 .
.
Полученная формула ничем не отличается от формулы для случая теплообмена между двумя телами с плоскопараллельными поверхностями.
2. Если 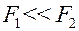 , то
, то 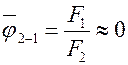 .
.
В этом случае формула упростится и примет вид

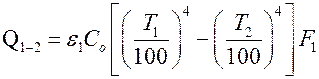 .
.
 2014-04-09
2014-04-09 2391
2391








