Статистическое наблюдение или сбор статистических данных на сплошной или несплошной основе является первым этапом статистического исследования. В то же время такой вид несплошного наблюдения, как наблюдение выборочное основан на теории относительных и средних показателей, показателей вариации, предельных теоремах закона больших чисел. Поэтому приступать к изучению данной темы, к решению учебных и практических задач можно только после того, как будет пройден и усвоен материал предшествующих тем данного курса.
Выборочным называется такое несплошное наблюдение, при котором признаки регистрируются у отдельных единиц изучаемой статистической совокупности, отобранных с использованием специальных методов, а полученные в процессе обследования результаты с определенным уровнем вероятности распространяются на всю исходную совокупность. К наиболее распространенным на практике видам выборочного наблюдения относятся:
· собственно-случайная (простая случайная) выборка;
· механическая (систематическая) выборка;
· типическая (стратифицированная, расслоенная) выборка;
· серийная (гнездовая) выборка.
Отбор единиц в выборочную совокупность может быть повторным или бесповторным. При повторном отборе попавшая в выборку единица подвергается обследованию, т.е. регистрации значений ее признаков, возвращается в генеральную совокупность и наравне с другими единицами участвует в дальнейшей процедуре отбора. При бесповторном отборе попавшая в выборку единица подвергается обследованию и в дальнейшей процедуре отбора не участвует
Выборочное наблюдение, как бы грамотно с методологической точки зрения оно ни было организовано, всегда связано с определенными, пусть небольшими и измеряемыми ошибками. Случайные ошибки выборки обусловлены действием случайных факторов, не содержащих каких-либо элементов системности в направлении воздействия на рассчитываемые выборочные характеристики. Даже при строгом соблюдении всех принципов формирования выборочной совокупности выборочные и генеральные характеристики будут несколько различаться. Поэтому получаемые случайные ошибки должны быть статистически оценены и учтены при распространении результатов выборочного наблюдения на всю генеральную совокупность. Оценка таких ошибок и является основной задачей, решаемой в теории выборочного наблюдения. Обратной задачей является определение такой минимально необходимой численности выборочной совокупности, при которой ошибка не превысит заданной величины. На выработку навыков в решении этих задач и направлен материал данной главы.
Собственно-случайная выборка. Ее суть заключается в отборе единиц из генеральной совокупности в целом, без разделения ее на группы, подгруппы или серии отдельных единиц. При этом единицы отбираются в случайном порядке, не зависящем ни от последовательности расположения единиц в совокупности, ни от значений их признаков.
После проведения отбора с использованием одного из алгоритмов, реализующих принцип случайности, или на основе таблицы случайных чисел, определяются границы генеральных характеристик. Для этого рассчитываются средняя и предельная ошибки выборки.
Средняя ошибка повторной собственно-случайной выборки определяется по формуле:
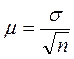
где σ - среднее квадратическое отклонение изучаемого признака;
n – объем (число единиц) выборочной совокупности.
Предельная ошибка выборки связана с заданным уровнем вероятности. При решении представленных ниже задач требуемая вероятность составляет 0,954 (t = 2) или 0,997 (t = 3). С учетом выбранного уровня вероятности и соответствующего ему значения t предельная ошибка выборки составит:
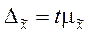
Тогда можно утверждать, что при заданной вероятности средняя генеральной совокупности будет находиться в следующих границах:
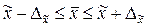
При определении границ генеральной доли при расчете средней ошибки выборки используется дисперсия альтернативного признака, которая вычисляется по следующей формуле:
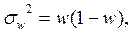
где w – выборочная доля, т. е. доля единиц, обладающих определенным вариантом или вариантами изучаемого признака.
При решении отдельных задач необходимо учитывать, что при неизвестной дисперсии альтернативного признака можно использовать ее максимально возможную величину, равную 0,25.
Пример. В результате выборочного обследования незанятого населения, ищущего работу, осуществленного на основе собственно-случайной повторной выборки, получен следующий ряд распределения (табл.).
Внимание! Если в задании необходимо осуществить выборку их генеральной совокупности (например, в исходной таблице приведены 77 территорий из которых необходимо сделать 13% -ю бесповторную выборку). Для отбора можно использовать возможности Excel – «Генератор случайных чисел». Алгоритм отбора следующий:
 2015-01-30
2015-01-30 1741
1741
