Задание 2. На одном графике построить 3 кривые: соответствующую первому слагаемому (красная пунктирная линия), соответствующую второму слагаемому (зеленая линия типа точка-тире), соответствующую результату сложения (черная сплошная) (3 периода).
| № варианта | Задание | Тип линии |
| 1. | Окружность радиуса r с центром в начале координат x = r cos t, y = r sin t, t =[0,2 π) | черная сплошная без маркера |
| 2. | Эллипс с большой и малой полуосями соответственно r 1 и r 2 и расположенными параллельно осям координат x = r 1cos t, y = r 2sin t, t =[0,2 π) | черная пунктирная без маркера |
| 3. | Улитка Паскаля x = a cos2 t + b cos t, y = a cos t sin t + b sin t, t =[0,2 π) при a > b. | черная линия типа точка-тире без маркера |
| 4. | Улитка Паскаля x = a cos2 t + b cos t, y = a cos t sin t + b sin t, t =[0,2 π) при b >2 a. | черная сплошная с маркером типа круг |
| 5. | Улитка Паскаля x = a cos2 t + b cos t, y = a cos t sin t + b sin t, t =[0,2 π) при a < b <2 a. | черная пунктирная с маркером типа квадрат |
| 6. | Кардиоида x = a cos t (1+cos t), y = a sin t (1+cos t), t =[0,2 π) при a >0. | синяя сплошная без маркера |
| 7. | Эпициклоида x =(a+b)cos t - a cos((a + b) t / a), y =(a+b)sin t - a sin((a + b) t / a), t =[0,2 π) при a >0. b >0, b / a – целое число. | синяя пунктирная без маркера |
| 8. | Эпициклоида x =(a+b)cos t - a cos((a + b) t / a), y =(a+b)sin t - a sin((a + b) t / a), t =[0,2 π) при a >0. b >0, b / a = p / q >1, где p и q – взаимно простые целые числа t =[0,2 qπ). | синяя линия типа точка-тире без маркера |
| 9. | Астроида x = b cos3 t, y = b sin3 t, t =[0,2 π) | синяя сплошная с маркером типа круг |
| 10. | Строфоида x = a (t 2-1)/(t 2+1), y = at (t 2-1)/(t 2+1), a >0, t =[- a, a ]. | синяя пунктирная с маркером типа квадрат |
| 11. | Окружность радиуса r с центром в начале координат x = r cos t, y = r sin t, t =[0,2 π) | красная пунктирная с маркером типа квадрат |
| 12. | Эллипс с большой и малой полуосями соответственно r 1 и r 2 и расположенными параллельно осям координат x = r 1cos t, y = r 2sin t, t =[0,2 π) | красная сплошная с маркером типа круг |
| 13. | Улитка Паскаля x = a cos2 t + b cos t, y = a cos t sin t + b sin t, t =[0,2 π) при a > b. | красная линия типа точка-тире без маркера |
| 14. | Улитка Паскаля x = a cos2 t + b cos t, y = a cos t sin t + b sin t, t =[0,2 π) при b >2 a. | красная сплошная без маркера |
| 15. | Улитка Паскаля x = a cos2 t + b cos t, y = a cos t sin t + b sin t, t =[0,2 π) при a < b <2 a. | красная пунктирная без маркера |
| 16. | Кардиоида x = a cos t (1+cos t), y = a sin t (1+cos t), t =[0,2 π) при a >0. | желтая пунктирная с маркером типа квадрат |
| 17. | Эпициклоида x =(a+b)cos t - a cos((a + b) t / a), y =(a+b)sin t - a sin((a + b) t / a), t =[0,2 π) при a >0. b >0, b / a – целое число. | желтая сплошная с маркером типа круг |
| 18. | Эпициклоида x =(a+b)cos t - a cos((a + b) t / a), y =(a+b)sin t - a sin((a + b) t / a), t =[0,2 π) при a >0. b >0, b / a = p / q >1, где p и q – взаимно простые целые числа t =[0,2 qπ). | желтая линия типа точка-тире без маркера |
| 19. | Астроида x = b cos3 t, y = b sin3 t, t =[0,2 π) | желтая сплошная без маркера |
| 20. | Строфоида x = a (t 2-1)/(t 2+1), y = at (t 2-1)/(t 2+1), a >0, t =[- a, a ]. | желтая пунктирная без маркера |
| 21. | Окружность радиуса r с центром в начале координат x = r cos t, y = r sin t, t =[0,2 π) | зеленая линия типа точка-тире без маркера |
| 22. | Эллипс с большой и малой полуосями соответственно r 1 и r 2 и расположенными параллельно осям координат x = r 1cos t, y = r 2sin t, t =[0,2 π) | зеленая сплошная с маркером типа круг |
| 23. | Улитка Паскаля x = a cos2 t + b cos t, y = a cos t sin t + b sin t, t =[0,2 π) при a > b. | зеленая сплошная без маркера |
| 24. | Улитка Паскаля x = a cos2 t + b cos t, y = a cos t sin t + b sin t, t =[0,2 π) при b >2 a. | зеленая пунктирная без маркера |
| 25. | Улитка Паскаля x = a cos2 t + b cos t, y = a cos t sin t + b sin t, t =[0,2 π) при a < b <2 a. | зеленая пунктирная с маркером типа круг |
| 26. | Кардиоида x = a cos t (1+cos t), y = a sin t (1+cos t), t =[0,2 π) при a >0. | синяя линия типа точка-тире без маркера |
| 27. | Эпициклоида x =(a+b)cos t - a cos((a + b) t / a), y =(a+b)sin t - a sin((a + b) t / a), t =[0,2 π) при a >0. b >0, b / a – целое число. | желтая сплошная с маркером типа круг |
| 28. | Эпициклоида x =(a+b)cos t - a cos((a + b) t / a), y =(a+b)sin t - a sin((a + b) t / a), t =[0,2 π) при a >0. b >0, b / a = p / q >1, где p и q – взаимно простые целые числа t =[0,2 qπ). | красная сплошная без маркера |
| 29. | Астроида x = b cos3 t, y = b sin3 t, t =[0,2 π) | желтая пунктирная без маркера |
| 30. | Строфоида x = a (t 2-1)/(t 2+1), y = at (t 2-1)/(t 2+1), a >0, t =[- a, a ]. | черная пунктирная с маркером типа круг |
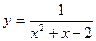
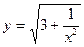
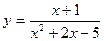
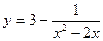
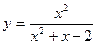
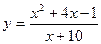
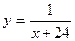
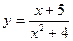
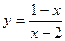
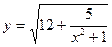
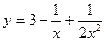
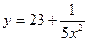
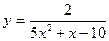
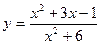
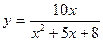
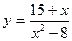
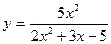
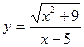
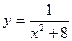
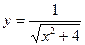
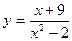
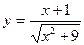
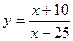
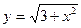
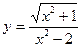
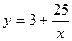
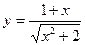
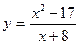
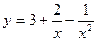
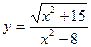
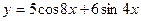
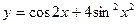
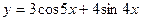
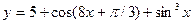
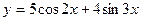
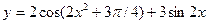
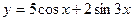
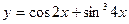
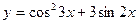
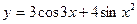
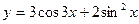
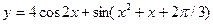
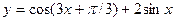
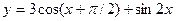
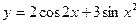
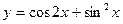
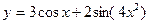
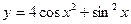
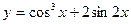
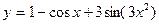
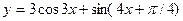
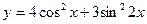
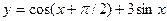
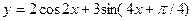
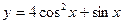
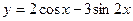
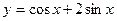
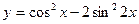
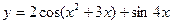
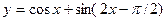
 2015-01-30
2015-01-30 1223
1223
