Всякое твердое тело можно рассматривать как систему из n материальных точек и масса m тела есть сумма масс всех этих точек:
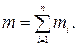
Будем считать, что тело абсолютно твердое, т.е. расстояния между любыми двумя его материальными точками не изменяются в процессе движения.
Рассмотрим движение твердого тела, закрепленного о одной неподвижной точке О, вокруг которой тело может свободно вращаться. Эта точка называется центром вращения тела. Совместим с этой точкой начало неподвижной системы координат. Тогда положение в пространстве i -точки тела определяется радиусом-вектором 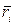 , проведенным из центра О в эту точку (рис. 4.1).
, проведенным из центра О в эту точку (рис. 4.1).
 Обозначим через
Обозначим через 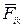 силу, действующую на i -ю точку тела со стороны k -ой его точки, и через
силу, действующую на i -ю точку тела со стороны k -ой его точки, и через 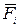 – равнодействующую всех внешних сил, приложенных к i -й точке. По второму закону Ньютона уравнение движения этой материальной точки имеет следующий вид:
– равнодействующую всех внешних сил, приложенных к i -й точке. По второму закону Ньютона уравнение движения этой материальной точки имеет следующий вид:

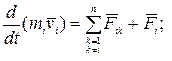
(k≠i, т.к. i -я точка сама на себя не действует).
Умножим обе части этого уравнения векторно на 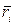 :
:
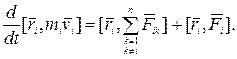 (4.1)
(4.1)
Векторное произведение радиуса-вектора 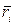 материальной точки на ее импульс
материальной точки на ее импульс 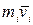 называется моментом импульса
называется моментом импульса 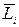 этой материальной точки относительно точки О:
этой материальной точки относительно точки О:
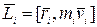 . (4.2)
. (4.2)
Вектор 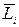 называют также моментом количества движения материальной точки. Он направлен перпендикулярно к плоскости, проведенной через векторы
называют также моментом количества движения материальной точки. Он направлен перпендикулярно к плоскости, проведенной через векторы 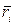 и
и 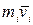 , и образует с ними правую тройку векторов: при наблюдении из конца
, и образует с ними правую тройку векторов: при наблюдении из конца 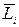 видно, что вращение от
видно, что вращение от 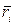 к
к 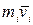 по кратчайшему расстоянию происходит против часовой стрелки.
по кратчайшему расстоянию происходит против часовой стрелки.
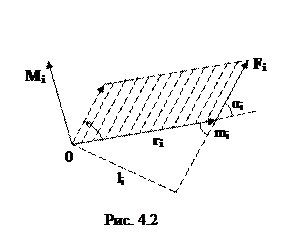
Векторное произведение радиуса-вектора 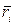 , проведенного из центра О в точку приложения внешней силы
, проведенного из центра О в точку приложения внешней силы 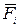 (рис. 4.2), на эту силу, называется моментом
(рис. 4.2), на эту силу, называется моментом 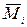 силы
силы 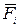 относительно точки О:
относительно точки О:
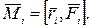 (4.3)
(4.3)
 Векторы
Векторы 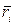 ,
, 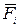 и
и 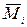 также образуют правую тройку. Модуль момента силы, как следует из рисунка, равен:
также образуют правую тройку. Модуль момента силы, как следует из рисунка, равен:

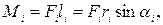
где li – плечо силы 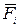 , т.е. длина перпендикуляра, опущенного из точки О на линию действия силы.
, т.е. длина перпендикуляра, опущенного из точки О на линию действия силы.
Моментом инерции тела относительно оси вращения называется физическая величина, равная сумме произведений масс n материальных точек тела на квадраты их расстояний до рассматриваемой оси:
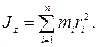 (4.4)
(4.4)
В случае непрерывного распределения масс эта сумма сводится к интегралу
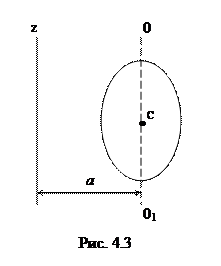
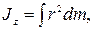
где интегрирование производится по всему объему тела. Величина r в данном случае есть функция положения точки с координатами x, y, z.
Неподвижная ось вращения z может проходить как через центр инерции тела (ось вращения маховика, ротора турбины и т.п.), так и вне его (например, ось вращения самолета, выполняющего мертвую петлю). Если известен момент инерции тела относительно оси, проходящей через его центр масс (инерции), то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера (теоремой о переносе осей инерции): момент инерции тела J z относительно произвольной оси вращения z равен сумме момента инерции тела относительно оси ОО1, проведенной через центр инерции С тела параллельно оси z и произведения массы тела на квадрат расстояния между этими осями (рис. 4.3):
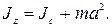 (4.5)
(4.5)
Таким образом, с удалением центра инерции тела от его оси вращения момент инерции тела относительно этой оси возрастает. Из формул (4.4) и (4.5) видно, что момент инерции тела зависит не только от его массы, но и от ее распределения относительно оси вращения.
В табл. 4.1 приведены значения моментов инерции для некоторых однородных тел.
Таблица 4.1
| Тело | Положение оси вращения | Момент инерции |
| Полый тонкостенный цилиндр радиуса R | Ось симметрии | 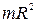 |
| Сплошной цилиндр или диск радиуса R | То же | 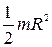 |
| Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его середину | 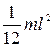 |
| Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его конец | 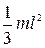 |
| Шар радиусом R | Ось проходит через центр шара | 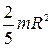 |
 2014-03-26
2014-03-26 2607
2607








