- Математическое ожидание постоянной случайной величины равно самой постоянной, т.е.
М(С)=С,
где С – некоторое число.
(Постоянной случайной величиной С называется такая случайная величина, которая принимает единственное значение равное С с вероятностью 1.)
- Постоянный множитель можно выносить за знак математического ожидания, т.е.
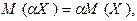
где 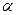 – произвольное число.
– произвольное число.
- Математическое ожидание суммы (разности) случайных величин равно сумме (разности) математических ожиданий этих случайных величин, т.е.
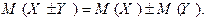
4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий, т.е.
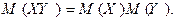
5. Пусть 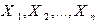 – такие случайные величины, математические ожидания которых равны между собой, т.е.
– такие случайные величины, математические ожидания которых равны между собой, т.е. 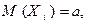 где
где 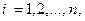 и а – некоторое число. Тогда среднее арифметическое этих случайных величин равно их общему математическому ожиданию, т.е.
и а – некоторое число. Тогда среднее арифметическое этих случайных величин равно их общему математическому ожиданию, т.е.
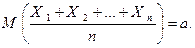
Заметим, что свойства 2 – 5 математического ожидания остаются справедливыми также для непрерывных случайных величин.
Пусть закон распределения случайной величины Х тот же, что и выше (см. начало параграфа).
Определение. Дисперсией дискретной случайной величины Х называется число 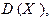 определяемое равенством
определяемое равенством
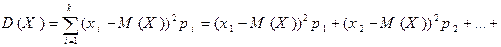
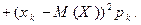
Число 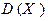 является мерой разброса значений случайной величины Х около ее математического ожидания.
является мерой разброса значений случайной величины Х около ее математического ожидания.
Пример. Пусть случайная величина Х биномиально распределена с параметрами 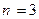 и
и 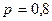 . Найдем дисперсию этой случайной величины.
. Найдем дисперсию этой случайной величины.
В предыдущем примере найдено, что М(Х) = 2,4. Тогда
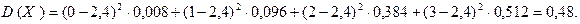
 2015-01-30
2015-01-30 502
502








