Определение. Функцией распределения случайной величины Х называется такая функция 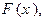 значение которой в точке x численно равно вероятности того, что в произвольном испытании значение случайной величины Х окажется меньше чем х, т.е.
значение которой в точке x численно равно вероятности того, что в произвольном испытании значение случайной величины Х окажется меньше чем х, т.е.
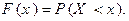
Данное определение задает функцию распределения не только для дискретных, но и для непрерывных случайных величин.
Пример. Пусть закон распределения случайной величины Х имеет вид
| X: | 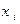
| ||
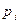
| 0,3 | 0,7 |
Найти функцию распределения этой случайной величины.
Решение. Найдем сначала F(x) для некоторых значений переменной х. Например,
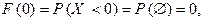
так как данная случайная величина не имеет значений меньших нуля, а потому событие (Х < 0) для нее является невозможным. Аналогично, при любом значении переменной х, которое менее или равно 1,будем иметь 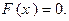 Далее имеем:
Далее имеем:
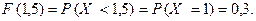
Аналогично, при любом значении переменной х таком, что 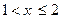 ,будем иметь
,будем иметь 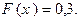
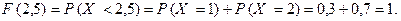
(Или, другими словами, так как все значения данной случайной величины менее 2,5, то событие (Х < 2,5) является достоверным, а потому его вероятность равна 1.) Аналогично, при любом значении переменной х, которое более или равно 2,будем иметь 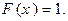
Окончательно имеем:
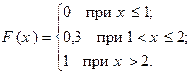
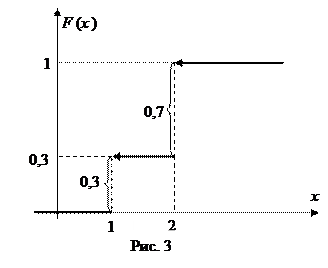 График найденной функции распределения изображен на рис. 3.
График найденной функции распределения изображен на рис. 3.
 2015-01-30
2015-01-30 508
508








