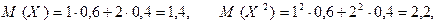

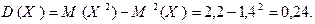
Математическое ожидание и дисперсия случайной величины называются параметрами распределения этой случайной величины.
Теорема. Пусть случайная величина 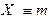 – б иномиально распределена с параметрами
– б иномиально распределена с параметрами 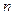 и p, тогда параметры ее распределения могут быть найдены по формулам:
и p, тогда параметры ее распределения могут быть найдены по формулам:

Также справедливы равенства
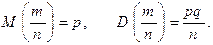
Пример. Пусть случайная величина Х биномиально распределена с параметрам 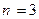 и
и 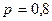 . Тогда
. Тогда
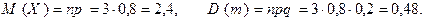
Очевидно, что использование формул последней теоремы упрощает и ускоряет вычисление математического ожидания и дисперсии биномиально распределенной случайной величины по сравнению с применением исходных определений для М(Х) и 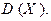
 2015-01-30
2015-01-30 444
444








