2015-01-30
543
- Дисперсия постоянной случайной величины равна нулю, т.е.
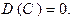
- Постоянный множитель можно выносить за знак дисперсии, возводя его при этом в квадрат, т.е.
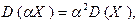
где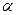 
– произвольное число.
- Справедливо равенство:
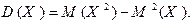
- Дисперсия суммы (разности) двух независимых случайных величин равна сумме дисперсий этих случайных величин, т.е.
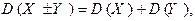
где случайные величины Х и Y – независимы.
- Пусть случайные величины
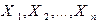– независимы и 
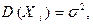где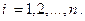 
Тогда
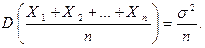
Замечание.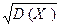 
называется средним квадратическим отклонением случайной величины Х и обычно обозначается через 
.
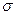Отметим также, что свойство 3 дисперсии более удобно для ее вычисления по сравнению с исходным определением дисперсии.
Пример. Пусть закон распределения случайной величины Х имеет вид
| X: |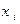 
| ||
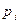
| 0,6 | 0,4 |
Найти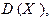 
используя свойство 3 дисперсии.
