Пример решения задачи 2

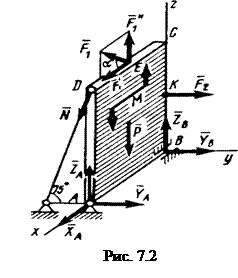
Вертикальная прямоугольная плита весом Р (рис. 7.2) закреплена сферическим шарниром в точке А, цилиндрическим (подшипником) в точке В и невесомым стержнем DD', лежащим в плоскости, параллельной плоскости yz. На плиту действуют сила 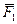, (в плоскости xz), сила 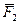(параллельная оси у) и пара сил с моментом М (в плоскости плиты).

Дaнo: Р = 5 кH; M = З кH·м; F₁ = 6 кH; F₂ = 7,5 кН; α = 30°; АВ = 1 м; ВС = 2 м; СЕ = 0,5 AB; ВК = 0,5 ВС.

Определить: реакции опор А, В и стержня DD'.

Решение

Рассмотрим равновесие плиты. На нее действуют задан­ные силы 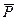, , 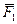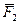и пара сил с моментом М, а также реакции связей. Реакцию сферического шарнира разложим на три составляющие 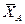, , 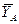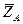; реакцию цилиндрического (подшипника) – на две составляющие 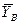, 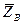(в плоскости, перпендикулярной оси подшипника), реакцию 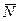стержня направим вдоль стержня, предполагая, что он растянут.

2. Для определения шести неизвестных реакций составляем шесть уравнений равновесия действующей на плиту пространственной системы сил:

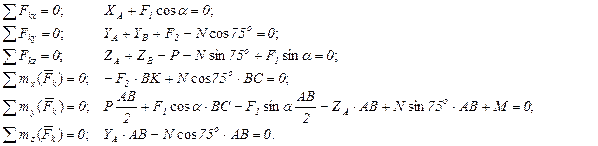
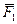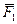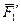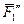Для определения момента силы , относительно оси у разлагаем , на составляющие и , параллельные осям х и z (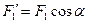; 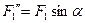), и применяем теорему Вариньона. Аналогично можно поступить при определении моментов реакции .

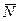Подставив в составленные уравнения числовые значения всех задан­ных величин и решив затем эти уравнения, найдем, чему равны искомые реакции.

Ответ: Х_A = -5,2 кН; Y_A = 3,8 кН; Z_A = 28,4 кН; Y_B = -7,5 кН; Z_B = -12,4 кН;
N = 14,5 кН. Знаки «минус» указывают, что силы 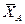, , 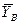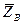направлены противоположно показанным на рис. 7.2.