2015-01-30
1650
В общем случае напряжения и деформации описываются тензорами второго ранга в трёхмерном пространстве (имеют по 9 компонент). Связывающий их тензор упругих постоянных является тензором четвёртого ранга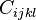 
и содержит 81 коэффициент. Вследствие симметрии тензора 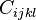, а также тензоров напряжений идеформаций, независимыми являются только 21 постоянная. Закон Гука выглядит следующим образом:
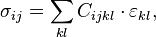
где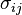 
— тензор напряжений, 
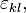— тензор деформаций. Для изотропного материала тензор 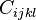содержит только два независимых коэффициента.
Благодаря симметрии тензоров напряжения и деформации, закон Гука может быть представлен в матричной форме.
Для линейно упругого изотропного тела:
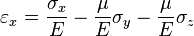
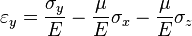
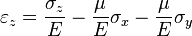
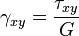
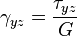
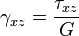
где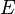 
— модуль Юнга,
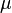— коэффициент Пуассона, 
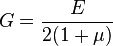— модуль сдвига.
