2015-01-30
1256
Сначала удобно найти полярный момент инерции Jp. Затем, учитывая, что для круга Jz = Jy, а Jp = Jz + Jy, найдем Jz = Jy = Jp /2.
Разобьем круг на бесконечно малые кольца толщиной d r и
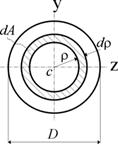радиусом r; площадь такого кольца
dA = 2 ×p ×r × d r. Подста-
вляя выражение для dA в выражение для Jp и интегрируя, получим
D /2
r4 D /2
p× D 4
|
тогда
A 0 4 0 32
|
Jz = J y = =.
2 64
2.3. Вычисление моментов инерции относительно параллельных осей
Пусть известны моменты инерции произвольного сечения относительно цен- тральных осей z и y:
Jz = ò
A
y 2× dA;
J y =
ò z 2 × dA;
A
Jzy
= ò z × y × dA.
A
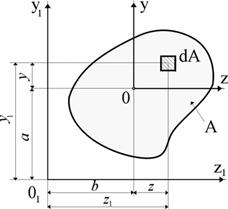Требуется определить моменты инерции этого сечения относительно «новых» осей z 1 и y 1, па- раллельных центральным и отстоящих от них на расстояние a и b соответственно:
|
A
dA;
J = z 2
|
A
dA;
J z y = z × y × dA.
|
Координаты любой точки в «новой» системе координат z 101 y 1можно выразить через координаты в «старых» осях z и y так:
z 1= z + b; y 1= y + a.
Подставляем эти значения в формулы для моментов инерции в «новых» осях и интегрируем почленно:
Jz 1
= ò y 2× dA =
ò(y + a)2× dA = ò
y 2× dA + 2 × a × ò
y × dA + a 2 × ò
dA,
Jz 1
= Jz + 2 × a × Sz
+ a 2× A.
Так как оси z и y – центральные, то Sz =0.
Окончательно можем записать формулы «перехода» при параллельном пере- носе осей:
A;
A;
|
Отметим, что координаты a и b необходимо подставлять с учетом их знака (в системе ко- ординат z 101 y 1).
2.4. Вычисление моментов инерции при повороте координатных осей
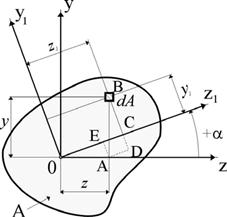Пусть известны моменты инерции произволь- ного сечения относительно центральных осей z, y:
Jz =
ò y 2 × dA;
A
J y =
ò z 2 × dA;
A
Jzy
= ò z × y × dA.
A
Повернем оси z, y на угол a против часовой стрелки, считая угол поворота осей в этом на- правлении положительным.
Требуется определить моменты инерции относительно «новых» (повернутых) осей z 1 и y 1:
|
A
dA;
J = z 2
|
A
dA;
J z y = z × y × dA.
|
Координаты элементарной площадки dA в «новой» системе координат z 10 y 1
можно выразить через координаты в «старых» осях так:
z 1= OC = OE + AD = z × cos a + y ×sin a;
y 1= BC = BD - EA = y × cos a - z ×sin a.
Подставляем эти значения в формулы для моментов инерции в «новых» осях и интегрируем почленно:
Jz 1
= ò y 2× dA =
ò(y × cos a - z × sin a)2× dA =
= cos2a × ò y 2× dA - 2 ×sin a×cosa× ò z × y × dA + sin2a × ò z 2× dA =
A A A
= J × cos2a + J
× sin2a - J
× sin 2a.
z y zy
Проделав аналогичные преобразования с остальными выражениями, запишем окончательно формулы «перехода» при повороте координатных осей:
J = J
× cos2a + J
×sin2a - J
× sin 2a; (2.1)
z 1 z y zy
J = J
× cos2a + J
×sin2a + J
× sin 2a; (2.2)
y 1 y z zy
J z 1 y 1
J - J
= z y ×sin 2a + J
2 zy
× cos 2a. (2.3)
Отметим, что если сложить два первых уравнения, то получим
|
т. е. полярный момент инерции есть величина инвариантная (другими словами, не- изменная при повороте координатных осей).
2.5. Главные оси и главные моменты инерции
До сих пор рассматривались геометрические характеристики сечений в произвольной сис- теме координат, однако наибольший практический интерес представляет система коорди- нат, в которой сечение описывается наименьшим количеством геометрических характери- стик. Такая «особая» система координат задается положением главных осей сечения. Вве- дем понятия: главные оси и главные моменты инерции.
Главные оси – две взаимно перпендикулярные оси, относительно которых центробежный момент инерции равен нулю, при этом осевые моменты инер- ции принимают экстремальные значения (максимум и минимум).
Главные оси, проходящие через центр тяжести сечения, называются глав - ными централ ь ными осями.
Моменты инерции относительно главных осей называются главными момен- тами инерции.
Главные центральные оси принято обозначать буквами u и v; главные момен- ты инерции – Ju и Jv (по определению Juv =0).
Выведем выражения, позволяющие находить положение главных осей и ве- личину главных моментов инерции. Зная, что Juv =0, воспользуемся уравнени- ем (2.3):
Отсюда
Juv=
Jz - J y
2
×sin 2a0+ Jzy × cos 2a0= 0.
2 × Jzy
tg 2a0= -
Jz - J y
. (2.4)
Угол a0 определяет положение главных осей относительно любых централь- ных осей z и y. Угол a0 откладывается между осью z и осью u и считается по- ложительным в направлении против часовой стрелки.
Заметим, что если сечение имеет ось симметрии, то, в соответствии со свойством центро- бежного момента инерции (см. разд.2.1, п.4), такая ось всегда будет главной осью сечения.
Исключая угол a в выражениях (2.1) и (2.2) с помощью (2.4), получим фор- мулы для определения главных осевых моментов инерции:
J + J 1
J = z y ±
(J - J
)2 + 4 × J 2.
max
min
2 2 z y yz
Запишем правило: ось максимум всегда составляет меньший угол с той из осей (z или y), относительно которой момент инерции имеет большее значе- ние.
