2015-01-30
605
Подобное движение газа наблюдается во впускном коллекторе карбюраторного двигателя, где подогрев осуществляется с целью испарения топливной пленки. Подводом теплоты к газу, движущемуся в трубе постоянного сечения, можно изменить скорость его движения. Процесс подвода теплоты вносит особый вид сопротивления – при подогреве движущегося газа полное давление падает.
Для получения зависимостей, связывающих изменение скорости с подводом теплоты (dQ), воспользуемся полученными ранее уравнениями:
× неразрывности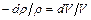 
;
× состояния в дифференциальной форме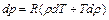 
.
Объединяя эти уравнения, получим
.
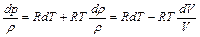С помощью уравнения Эйлера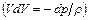 
исключим 
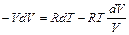
и преобразуем полученное уравнение
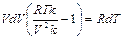. (2.57)
Правую часть заменим уравнением энергии
,
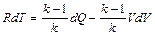после чего уравнение (2.57) примет вид
,
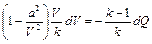или, использую число Маха, окончательно получим
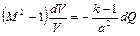. (2.58)
Из уравнения (2.58) следует, что при М < 1 подвод теплоты приводит к ускорению потока, отвод – к торможению его.
При М > 1 подвод теплоты приводит к торможению потока, отвод – к ускорению потока.
Подвод теплоты вызывает изменение температуры газа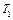 
и температуры изэнтропически заторможенного газа 
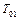, наблюдаемых до участка подогрева, на величину 
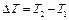, и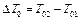 
, причем за участком прогрева вновь устанавливается адиабатическое течение с температурам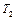и 
и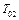 
.
Полагая, что приток теплоты не нарушает баланса массы и количества движения, для газа на участке подогрева воспользуемся уравнениями:
× неразрывности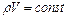 
;
× и импульсов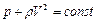 
.
Преобразуем эти уравнения к виду:
;
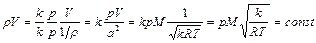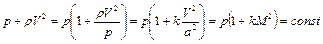. (2.59)
Разделим второе уравнение на первое и получим связь числа М с термодинамической температурой
.
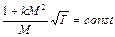Здесь постоянная величина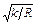 
объединена с const, стоящей в правой части.
Учитывая связь между термодинамической температурой Т и температурой адиабатически, изэнтропически заторможенного газа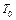 
получим
.
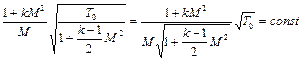Применим эти равенства к двум сечениям потока, ограничивающим участок подогрева,
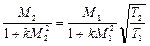. (2.60)
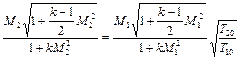. (2.61)
Приведем некоторые вычисления.
Предположим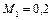 
, 
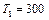К. Подводом теплоты поток ускоряется до 
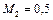. Определим температуру 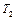по формуле (2.60).
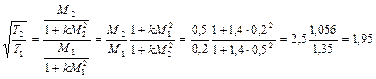
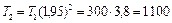К.
Предположим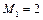 
, 
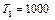К. Подводом теплоты поток замедляется до 
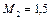. Определим температуру .
.
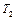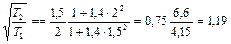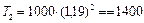К.
Подвод теплоты при любом движении увеличивает термодинамическую температуру и температуру торможения.
Для определения уменьшения давления и плотности зададимся соотношением температур
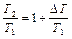
и числом М 1 до прохождения участка подогрева. По (2.60) найдем М 2, и затем по (2.59) отношение давлений
.
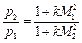Для определения соотношения плотностей применим уравнение состояния
.
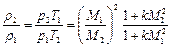В качестве примера выполним следующие расчеты.
Подводом теплоты при 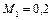поток разгоняется до 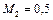. Определим изменение статического давления
.
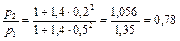Подводом теплоты при 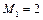поток замедляется до 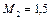. Соотношение давлений за счет этого изменится
.
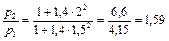При подводе теплоты к газу при М < 1 статическое давление падает, а при М > 1 возрастает.
При разгоне газа от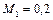 
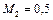до за счет подвода теплоты произойдет изменение плотности
.
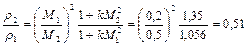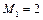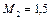При замедлении потока от до за счет подвода теплоты сотношение плотностей изменится
.
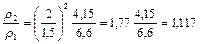При подводе теплоты к движущемуся газу при М < 1 плотность падает, а при М > 1 возрастает.
При значительных скоростях течения плотность газа при подогреве уменьшается не только из-за повышения температуры, но и вследствие понижения статического давления. В связи с этим скорость газа увеличивается вдоль трубы быстрее, чем температура. Скорость звука, которая ~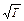 
, увеличивается вдоль трубы значительно медленнее, чем скорость потока. По этой причине число 
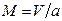по длине трубы растет при М < 1.
Поток, имеющий любую начальную скорость, можно за счет соответствующего подогрева довести до критической скорости (М 2 = 1). Но никаким подогревом нельзя перевести поток в цилиндрической трубе в сверхзвуковую область. Это явление носит название "тепловой кризис".
После того как в конце трубы достигается кризис, скорость потока в начале трубы не может быть увеличена никакими способами.
Если по достижению кризиса продолжать подогрев газа, то величина критической скорости в конце трубы растет, а скорость в начале трубы падает. То есть заданному количеству теплоты соответствует совершенно определенное предельное значение числа М в начале трубы.
Энтальпия («теплосодержание») заторможенного газа складывается из энтальпии в потоке и кинетической энергии:
; 
.
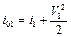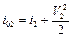Вследствие подвода теплоты энтальпия в конце трубы больше, чем в ее начале, на величину подведенного количества теплоты
.
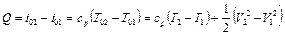Введем в рассмотрение функцию
.
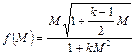Вычислим производную от этой функции
.
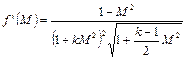Функция f (M) имеет максимум при М = 1, и этот максимум равен
.
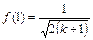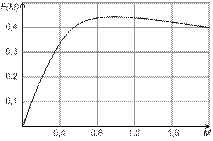На рисунке приведен график функции f (M) для воздуха (k = 1,4)
Как видно из графика и формулы (2.61) подогрев газа при М 1 < 1 вызывает возрастание функции f (M 2) и числа М 2, а при М 1 > 1, наоборот приводит к убыванию числа М 2. Следовательно, подвод теплоты к дозвуковому потоку ускоряет его, отвод теплоты – замедляет. В случае сверзвукового потока подвод теплоты замедляет его, а отвод – ускоряет.
Так, например, при Т 01 = 540К и М 1 = 0,5 увеличение температуры на 20% приводит к возрастанию числа М до значения М 2 = 0,6. При той же начальной температуре и числе М 1 = 1,4 подогрев газа на 7% приведет к уменьшению числа М до М 2 = 1. При этом давление увеличится более чем на 50%.
